355580
In the graph shown, the \(P.E\) of earth satellite system is shown by a solid line as a function of distance \(r\) (separation between centres). The total energy of the two objects which may or may not be bounded to the earth are shown in the figure with dotted lines.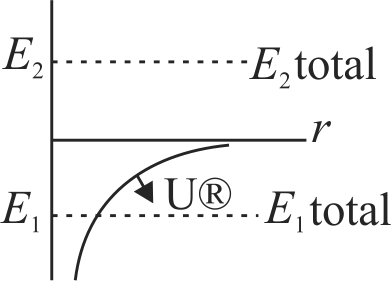
355580
In the graph shown, the \(P.E\) of earth satellite system is shown by a solid line as a function of distance \(r\) (separation between centres). The total energy of the two objects which may or may not be bounded to the earth are shown in the figure with dotted lines.
355580
In the graph shown, the \(P.E\) of earth satellite system is shown by a solid line as a function of distance \(r\) (separation between centres). The total energy of the two objects which may or may not be bounded to the earth are shown in the figure with dotted lines.
355580
In the graph shown, the \(P.E\) of earth satellite system is shown by a solid line as a function of distance \(r\) (separation between centres). The total energy of the two objects which may or may not be bounded to the earth are shown in the figure with dotted lines.
355580
In the graph shown, the \(P.E\) of earth satellite system is shown by a solid line as a function of distance \(r\) (separation between centres). The total energy of the two objects which may or may not be bounded to the earth are shown in the figure with dotted lines.

