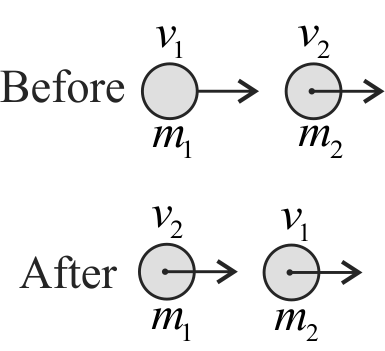
355260 Two masses ' \(m_{1}\) ' and ' \(m_{2}\) ' moving with velocities ' \(v_{1}\) ' and ' \(v_{2}\) ' in opposite directions collide elastically and after collision masses ' \(m_{1}{ }^{\prime}\) and ' \(m_{2}\) ' move with velocity ' \(v_{2}\) ' and ' \(v_{1}{ }^{\prime}\) respectively. The ratio \(\left(\dfrac{m_{1}}{m_{2}}\right)\) is

355261 A ball moving with a velocity \(v\) strikes a wall moving towards the ball with a velocity \(u\). An elastic impact lasts for \(t\) seconds then the mean elastic force acting on the ball is (Mass of the ball \(M\))

355262 A body of mass \(2\;kg\) makes an elastic collision with another body at rest and continues to move in the original direction with one-fourth its original speed. The mass of the second body which collides with the first body is

355263 A particle of mass \(m_{1}\) moves with velocity \(v_{1}\) and collides with another particle at rest of equal mass. The velocity of the second particle after the elastic collision is

355260 Two masses ' \(m_{1}\) ' and ' \(m_{2}\) ' moving with velocities ' \(v_{1}\) ' and ' \(v_{2}\) ' in opposite directions collide elastically and after collision masses ' \(m_{1}{ }^{\prime}\) and ' \(m_{2}\) ' move with velocity ' \(v_{2}\) ' and ' \(v_{1}{ }^{\prime}\) respectively. The ratio \(\left(\dfrac{m_{1}}{m_{2}}\right)\) is

355261 A ball moving with a velocity \(v\) strikes a wall moving towards the ball with a velocity \(u\). An elastic impact lasts for \(t\) seconds then the mean elastic force acting on the ball is (Mass of the ball \(M\))

355262 A body of mass \(2\;kg\) makes an elastic collision with another body at rest and continues to move in the original direction with one-fourth its original speed. The mass of the second body which collides with the first body is

355263 A particle of mass \(m_{1}\) moves with velocity \(v_{1}\) and collides with another particle at rest of equal mass. The velocity of the second particle after the elastic collision is

355260 Two masses ' \(m_{1}\) ' and ' \(m_{2}\) ' moving with velocities ' \(v_{1}\) ' and ' \(v_{2}\) ' in opposite directions collide elastically and after collision masses ' \(m_{1}{ }^{\prime}\) and ' \(m_{2}\) ' move with velocity ' \(v_{2}\) ' and ' \(v_{1}{ }^{\prime}\) respectively. The ratio \(\left(\dfrac{m_{1}}{m_{2}}\right)\) is

355261 A ball moving with a velocity \(v\) strikes a wall moving towards the ball with a velocity \(u\). An elastic impact lasts for \(t\) seconds then the mean elastic force acting on the ball is (Mass of the ball \(M\))

355262 A body of mass \(2\;kg\) makes an elastic collision with another body at rest and continues to move in the original direction with one-fourth its original speed. The mass of the second body which collides with the first body is

355263 A particle of mass \(m_{1}\) moves with velocity \(v_{1}\) and collides with another particle at rest of equal mass. The velocity of the second particle after the elastic collision is

355260 Two masses ' \(m_{1}\) ' and ' \(m_{2}\) ' moving with velocities ' \(v_{1}\) ' and ' \(v_{2}\) ' in opposite directions collide elastically and after collision masses ' \(m_{1}{ }^{\prime}\) and ' \(m_{2}\) ' move with velocity ' \(v_{2}\) ' and ' \(v_{1}{ }^{\prime}\) respectively. The ratio \(\left(\dfrac{m_{1}}{m_{2}}\right)\) is

355261 A ball moving with a velocity \(v\) strikes a wall moving towards the ball with a velocity \(u\). An elastic impact lasts for \(t\) seconds then the mean elastic force acting on the ball is (Mass of the ball \(M\))

355262 A body of mass \(2\;kg\) makes an elastic collision with another body at rest and continues to move in the original direction with one-fourth its original speed. The mass of the second body which collides with the first body is

355263 A particle of mass \(m_{1}\) moves with velocity \(v_{1}\) and collides with another particle at rest of equal mass. The velocity of the second particle after the elastic collision is