354868
Two uniform ropes of ratio of mass per unit length \(\eta\) (first to the second rope) are hanging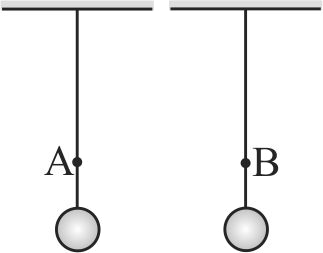
from the rigid supports. The different masses are attached to the free end of the rope such that tension at point \(A\) ( near to bottom) in the first rope and tension at \(B\) ( near the top) in the second rope are equal. Find the ratio of wavelengths of the pulses reaching at point \(A\) and \(B\), If ratio of the respective frequencies of the pulses produced at lower ends is \(\frac{1}{k}\)
354869 Two wires of different densities but same area of cross sections are soldered together at one end and are stretched at a tension \(T\). The velocity of a transverse wave in the first wire is double of that in the second wire. Find the ratio of the density of the first wire to that of the second wire.
354868
Two uniform ropes of ratio of mass per unit length \(\eta\) (first to the second rope) are hanging
from the rigid supports. The different masses are attached to the free end of the rope such that tension at point \(A\) ( near to bottom) in the first rope and tension at \(B\) ( near the top) in the second rope are equal. Find the ratio of wavelengths of the pulses reaching at point \(A\) and \(B\), If ratio of the respective frequencies of the pulses produced at lower ends is \(\frac{1}{k}\)
354869 Two wires of different densities but same area of cross sections are soldered together at one end and are stretched at a tension \(T\). The velocity of a transverse wave in the first wire is double of that in the second wire. Find the ratio of the density of the first wire to that of the second wire.
354868
Two uniform ropes of ratio of mass per unit length \(\eta\) (first to the second rope) are hanging
from the rigid supports. The different masses are attached to the free end of the rope such that tension at point \(A\) ( near to bottom) in the first rope and tension at \(B\) ( near the top) in the second rope are equal. Find the ratio of wavelengths of the pulses reaching at point \(A\) and \(B\), If ratio of the respective frequencies of the pulses produced at lower ends is \(\frac{1}{k}\)
354869 Two wires of different densities but same area of cross sections are soldered together at one end and are stretched at a tension \(T\). The velocity of a transverse wave in the first wire is double of that in the second wire. Find the ratio of the density of the first wire to that of the second wire.
354868
Two uniform ropes of ratio of mass per unit length \(\eta\) (first to the second rope) are hanging
from the rigid supports. The different masses are attached to the free end of the rope such that tension at point \(A\) ( near to bottom) in the first rope and tension at \(B\) ( near the top) in the second rope are equal. Find the ratio of wavelengths of the pulses reaching at point \(A\) and \(B\), If ratio of the respective frequencies of the pulses produced at lower ends is \(\frac{1}{k}\)
354869 Two wires of different densities but same area of cross sections are soldered together at one end and are stretched at a tension \(T\). The velocity of a transverse wave in the first wire is double of that in the second wire. Find the ratio of the density of the first wire to that of the second wire.
354868
Two uniform ropes of ratio of mass per unit length \(\eta\) (first to the second rope) are hanging
from the rigid supports. The different masses are attached to the free end of the rope such that tension at point \(A\) ( near to bottom) in the first rope and tension at \(B\) ( near the top) in the second rope are equal. Find the ratio of wavelengths of the pulses reaching at point \(A\) and \(B\), If ratio of the respective frequencies of the pulses produced at lower ends is \(\frac{1}{k}\)
354869 Two wires of different densities but same area of cross sections are soldered together at one end and are stretched at a tension \(T\). The velocity of a transverse wave in the first wire is double of that in the second wire. Find the ratio of the density of the first wire to that of the second wire.