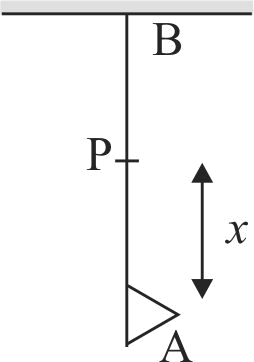
354873 A uniform rope length \(L\) and mass \(m_{1}\) hangs vertically from a rigid support. a block of mass \(m_{2}\) is attached to the free end of the rope. A transverse pulse of wavelength \(\lambda_{1}\) is produced at the lower end of the rope. The wavelength of the pulse when its reaches the top of the rope is \(\lambda_{2}\). the ratio \(\lambda_{2} / \lambda_{1}\) is.
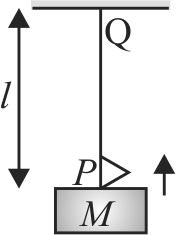
354873 A uniform rope length \(L\) and mass \(m_{1}\) hangs vertically from a rigid support. a block of mass \(m_{2}\) is attached to the free end of the rope. A transverse pulse of wavelength \(\lambda_{1}\) is produced at the lower end of the rope. The wavelength of the pulse when its reaches the top of the rope is \(\lambda_{2}\). the ratio \(\lambda_{2} / \lambda_{1}\) is.
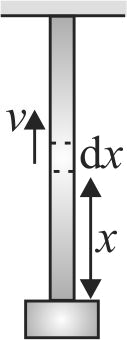
354873 A uniform rope length \(L\) and mass \(m_{1}\) hangs vertically from a rigid support. a block of mass \(m_{2}\) is attached to the free end of the rope. A transverse pulse of wavelength \(\lambda_{1}\) is produced at the lower end of the rope. The wavelength of the pulse when its reaches the top of the rope is \(\lambda_{2}\). the ratio \(\lambda_{2} / \lambda_{1}\) is.
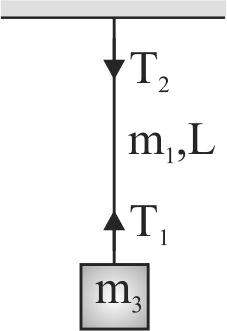
354873 A uniform rope length \(L\) and mass \(m_{1}\) hangs vertically from a rigid support. a block of mass \(m_{2}\) is attached to the free end of the rope. A transverse pulse of wavelength \(\lambda_{1}\) is produced at the lower end of the rope. The wavelength of the pulse when its reaches the top of the rope is \(\lambda_{2}\). the ratio \(\lambda_{2} / \lambda_{1}\) is.