354716
A source of sound emits sound waves at frequency \(f_{0}\). It is moving towards an observer with fixed speed \(v_{s}\left(v_{s} < v\right.\), where \(v\) is the speed of sound in air). If the observer were to move towards the source with speed \(v_{0}\), one of the following two graphs (\(A\) and \(B\)) will given the correct variation of the frequency \(f\) heard by the observer as \(v_{0}\) is changed.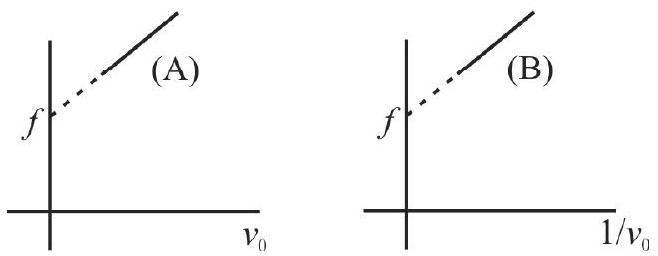
354716
A source of sound emits sound waves at frequency \(f_{0}\). It is moving towards an observer with fixed speed \(v_{s}\left(v_{s} < v\right.\), where \(v\) is the speed of sound in air). If the observer were to move towards the source with speed \(v_{0}\), one of the following two graphs (\(A\) and \(B\)) will given the correct variation of the frequency \(f\) heard by the observer as \(v_{0}\) is changed.
354716
A source of sound emits sound waves at frequency \(f_{0}\). It is moving towards an observer with fixed speed \(v_{s}\left(v_{s} < v\right.\), where \(v\) is the speed of sound in air). If the observer were to move towards the source with speed \(v_{0}\), one of the following two graphs (\(A\) and \(B\)) will given the correct variation of the frequency \(f\) heard by the observer as \(v_{0}\) is changed.
354716
A source of sound emits sound waves at frequency \(f_{0}\). It is moving towards an observer with fixed speed \(v_{s}\left(v_{s} < v\right.\), where \(v\) is the speed of sound in air). If the observer were to move towards the source with speed \(v_{0}\), one of the following two graphs (\(A\) and \(B\)) will given the correct variation of the frequency \(f\) heard by the observer as \(v_{0}\) is changed.
