359895
A particle of mass \(10\;g\) is kept on the surface of a uniform sphere of mass \(100\;g\) and radius \(10\;cm\). Find the work to be done against the gravitational force between them, to take the particle far away from the sphere.
(Take, \(G = 6.67 \times {10^{ - 11}}N{m^2}\;k{g^{ - 2}}\))
359896
A particle is projected from point \(A\), that is at a distance 4\(R\) from the centre of the Earth, with speed \(v_{1}\) in a direction making \(30^{\circ}\) with the line joining the centre of the Earth and point \(A\), as shown. Find the speed \(v_{1}\) of particle (in \(m/s\)) if particle passes grazing the surface of the earth. Consider gravitational interaction only between earth and the particle.
(use \(\frac{{GM}}{R} = 6.4 \times {10^7}\;{m^2}/{s^2}\))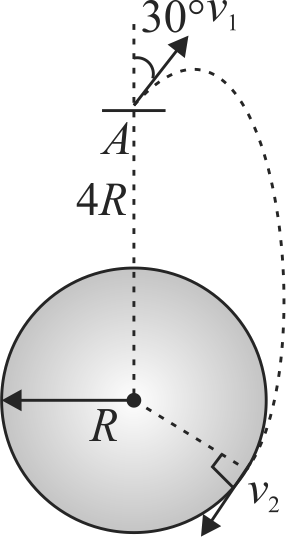
359895
A particle of mass \(10\;g\) is kept on the surface of a uniform sphere of mass \(100\;g\) and radius \(10\;cm\). Find the work to be done against the gravitational force between them, to take the particle far away from the sphere.
(Take, \(G = 6.67 \times {10^{ - 11}}N{m^2}\;k{g^{ - 2}}\))
359896
A particle is projected from point \(A\), that is at a distance 4\(R\) from the centre of the Earth, with speed \(v_{1}\) in a direction making \(30^{\circ}\) with the line joining the centre of the Earth and point \(A\), as shown. Find the speed \(v_{1}\) of particle (in \(m/s\)) if particle passes grazing the surface of the earth. Consider gravitational interaction only between earth and the particle.
(use \(\frac{{GM}}{R} = 6.4 \times {10^7}\;{m^2}/{s^2}\))
359895
A particle of mass \(10\;g\) is kept on the surface of a uniform sphere of mass \(100\;g\) and radius \(10\;cm\). Find the work to be done against the gravitational force between them, to take the particle far away from the sphere.
(Take, \(G = 6.67 \times {10^{ - 11}}N{m^2}\;k{g^{ - 2}}\))
359896
A particle is projected from point \(A\), that is at a distance 4\(R\) from the centre of the Earth, with speed \(v_{1}\) in a direction making \(30^{\circ}\) with the line joining the centre of the Earth and point \(A\), as shown. Find the speed \(v_{1}\) of particle (in \(m/s\)) if particle passes grazing the surface of the earth. Consider gravitational interaction only between earth and the particle.
(use \(\frac{{GM}}{R} = 6.4 \times {10^7}\;{m^2}/{s^2}\))
359895
A particle of mass \(10\;g\) is kept on the surface of a uniform sphere of mass \(100\;g\) and radius \(10\;cm\). Find the work to be done against the gravitational force between them, to take the particle far away from the sphere.
(Take, \(G = 6.67 \times {10^{ - 11}}N{m^2}\;k{g^{ - 2}}\))
359896
A particle is projected from point \(A\), that is at a distance 4\(R\) from the centre of the Earth, with speed \(v_{1}\) in a direction making \(30^{\circ}\) with the line joining the centre of the Earth and point \(A\), as shown. Find the speed \(v_{1}\) of particle (in \(m/s\)) if particle passes grazing the surface of the earth. Consider gravitational interaction only between earth and the particle.
(use \(\frac{{GM}}{R} = 6.4 \times {10^7}\;{m^2}/{s^2}\))
359895
A particle of mass \(10\;g\) is kept on the surface of a uniform sphere of mass \(100\;g\) and radius \(10\;cm\). Find the work to be done against the gravitational force between them, to take the particle far away from the sphere.
(Take, \(G = 6.67 \times {10^{ - 11}}N{m^2}\;k{g^{ - 2}}\))
359896
A particle is projected from point \(A\), that is at a distance 4\(R\) from the centre of the Earth, with speed \(v_{1}\) in a direction making \(30^{\circ}\) with the line joining the centre of the Earth and point \(A\), as shown. Find the speed \(v_{1}\) of particle (in \(m/s\)) if particle passes grazing the surface of the earth. Consider gravitational interaction only between earth and the particle.
(use \(\frac{{GM}}{R} = 6.4 \times {10^7}\;{m^2}/{s^2}\))
