359897
Two hypothetical planets of masses \({m_1}\) and \({m_2}\) are at rest when they are infinite distance apart. Because of the gravitational force they move towards each other along the line joining their centres. What is their speed when their separation is ' \(d\) '? (Speed of \(m_{1}\) is \(v_{1}\) and that of \({m_2}\) is \({v_2}\)):-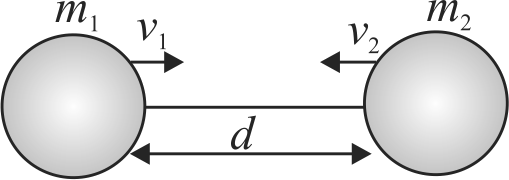
359897
Two hypothetical planets of masses \({m_1}\) and \({m_2}\) are at rest when they are infinite distance apart. Because of the gravitational force they move towards each other along the line joining their centres. What is their speed when their separation is ' \(d\) '? (Speed of \(m_{1}\) is \(v_{1}\) and that of \({m_2}\) is \({v_2}\)):-
359897
Two hypothetical planets of masses \({m_1}\) and \({m_2}\) are at rest when they are infinite distance apart. Because of the gravitational force they move towards each other along the line joining their centres. What is their speed when their separation is ' \(d\) '? (Speed of \(m_{1}\) is \(v_{1}\) and that of \({m_2}\) is \({v_2}\)):-
359897
Two hypothetical planets of masses \({m_1}\) and \({m_2}\) are at rest when they are infinite distance apart. Because of the gravitational force they move towards each other along the line joining their centres. What is their speed when their separation is ' \(d\) '? (Speed of \(m_{1}\) is \(v_{1}\) and that of \({m_2}\) is \({v_2}\)):-
