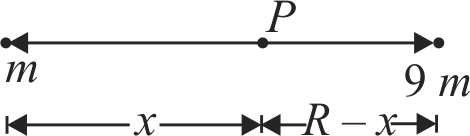
359871 From a solid sphere of mass \(M\) and radius \(R\), a spherical portion of radius \(\dfrac{R}{2}\) is removed, as shown in the figure. Taking gravitational potential \(V=0\) at \(r=\infty\), the potential at the centre of the cavity thus formed is
(\(G=\) Gravitational constant)

359872 A particle of mass \(M\) is situated at the centre of a spherical shell of same mass and radius \(a\). The gravitational potential at a point situated at \(a / 2\) distance from the centre, will be

359873 Two bodies of mass \(m\) and \(9 m\) are placed at a distance \(R\). The gravitational potential on the line joining the bodies where the gravitational field equals zero, will be ( \(G=\) gravitational constant):

359874 If \(V\) is the gravitational potential due to sphere of uniform density on it's surface, then its value at the centre of sphere will be

359871 From a solid sphere of mass \(M\) and radius \(R\), a spherical portion of radius \(\dfrac{R}{2}\) is removed, as shown in the figure. Taking gravitational potential \(V=0\) at \(r=\infty\), the potential at the centre of the cavity thus formed is
(\(G=\) Gravitational constant)

359872 A particle of mass \(M\) is situated at the centre of a spherical shell of same mass and radius \(a\). The gravitational potential at a point situated at \(a / 2\) distance from the centre, will be

359873 Two bodies of mass \(m\) and \(9 m\) are placed at a distance \(R\). The gravitational potential on the line joining the bodies where the gravitational field equals zero, will be ( \(G=\) gravitational constant):

359874 If \(V\) is the gravitational potential due to sphere of uniform density on it's surface, then its value at the centre of sphere will be

359871 From a solid sphere of mass \(M\) and radius \(R\), a spherical portion of radius \(\dfrac{R}{2}\) is removed, as shown in the figure. Taking gravitational potential \(V=0\) at \(r=\infty\), the potential at the centre of the cavity thus formed is
(\(G=\) Gravitational constant)

359872 A particle of mass \(M\) is situated at the centre of a spherical shell of same mass and radius \(a\). The gravitational potential at a point situated at \(a / 2\) distance from the centre, will be

359873 Two bodies of mass \(m\) and \(9 m\) are placed at a distance \(R\). The gravitational potential on the line joining the bodies where the gravitational field equals zero, will be ( \(G=\) gravitational constant):

359874 If \(V\) is the gravitational potential due to sphere of uniform density on it's surface, then its value at the centre of sphere will be

359871 From a solid sphere of mass \(M\) and radius \(R\), a spherical portion of radius \(\dfrac{R}{2}\) is removed, as shown in the figure. Taking gravitational potential \(V=0\) at \(r=\infty\), the potential at the centre of the cavity thus formed is
(\(G=\) Gravitational constant)

359872 A particle of mass \(M\) is situated at the centre of a spherical shell of same mass and radius \(a\). The gravitational potential at a point situated at \(a / 2\) distance from the centre, will be

359873 Two bodies of mass \(m\) and \(9 m\) are placed at a distance \(R\). The gravitational potential on the line joining the bodies where the gravitational field equals zero, will be ( \(G=\) gravitational constant):

359874 If \(V\) is the gravitational potential due to sphere of uniform density on it's surface, then its value at the centre of sphere will be