359596
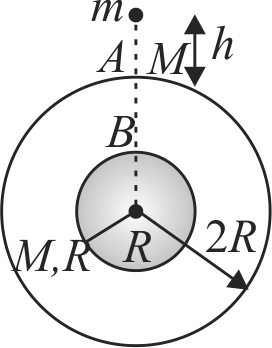
A solid sphere of mass \(M\) and radius \(R\) is surrounded by a spherical shell of same mass \(M\) and radius 2\(R\) as shown. A small particle of mass \(m\) is released from rest from a height \(h( < < R)\) above the shell. There is a hole in the shell. In what time will it enter the hole at \(A\)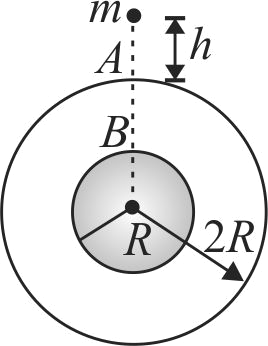
359596
A solid sphere of mass \(M\) and radius \(R\) is surrounded by a spherical shell of same mass \(M\) and radius 2\(R\) as shown. A small particle of mass \(m\) is released from rest from a height \(h( < < R)\) above the shell. There is a hole in the shell. In what time will it enter the hole at \(A\)
359596
A solid sphere of mass \(M\) and radius \(R\) is surrounded by a spherical shell of same mass \(M\) and radius 2\(R\) as shown. A small particle of mass \(m\) is released from rest from a height \(h( < < R)\) above the shell. There is a hole in the shell. In what time will it enter the hole at \(A\)
359596
A solid sphere of mass \(M\) and radius \(R\) is surrounded by a spherical shell of same mass \(M\) and radius 2\(R\) as shown. A small particle of mass \(m\) is released from rest from a height \(h( < < R)\) above the shell. There is a hole in the shell. In what time will it enter the hole at \(A\)
359596
A solid sphere of mass \(M\) and radius \(R\) is surrounded by a spherical shell of same mass \(M\) and radius 2\(R\) as shown. A small particle of mass \(m\) is released from rest from a height \(h( < < R)\) above the shell. There is a hole in the shell. In what time will it enter the hole at \(A\)