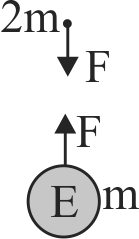
359599
In order to simulate different values of \(g\), aspiring astronauts are put on a plane which dives in a parabola given by the equation:
\(x^{2}=500 y\)
Where \(x\) is horizontal, \(y\) is vertically upwards; both being measured of the velocity of the plane is constant throughout, and has the value of 360 \(km/h\). The effective \(g\) experienced by an astronaut on the plane equals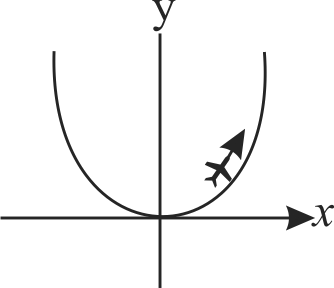
359599
In order to simulate different values of \(g\), aspiring astronauts are put on a plane which dives in a parabola given by the equation:
\(x^{2}=500 y\)
Where \(x\) is horizontal, \(y\) is vertically upwards; both being measured of the velocity of the plane is constant throughout, and has the value of 360 \(km/h\). The effective \(g\) experienced by an astronaut on the plane equals
359599
In order to simulate different values of \(g\), aspiring astronauts are put on a plane which dives in a parabola given by the equation:
\(x^{2}=500 y\)
Where \(x\) is horizontal, \(y\) is vertically upwards; both being measured of the velocity of the plane is constant throughout, and has the value of 360 \(km/h\). The effective \(g\) experienced by an astronaut on the plane equals
359599
In order to simulate different values of \(g\), aspiring astronauts are put on a plane which dives in a parabola given by the equation:
\(x^{2}=500 y\)
Where \(x\) is horizontal, \(y\) is vertically upwards; both being measured of the velocity of the plane is constant throughout, and has the value of 360 \(km/h\). The effective \(g\) experienced by an astronaut on the plane equals