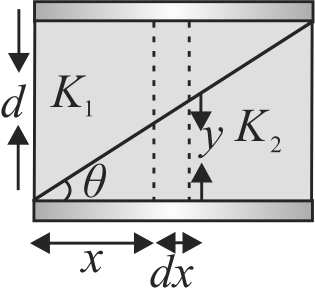
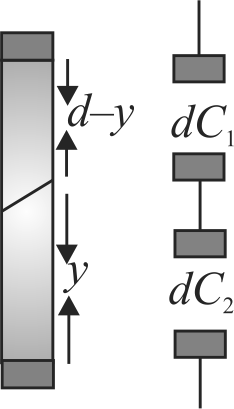
359207
A parallel plate capacitor has plates of area \(A\) separted by distance \(‘d’\) between them. It is filled with a dielectric which has a dielectric constant that varies as \(k\left( x \right) = K\left( {1 + \alpha x} \right)\) where \(‘x’\) is the distance measured from one of the plates. If \(\left( {\alpha d} \right) < < 1\), the total capacitance of the system is best given by the expression :
359209
Assertion :
A parallel plate capacitor is charged to a potential difference of \(100\;V\), and disconnected from the voltage source. A slab of dielectric is then slowly inserted between the plates. Then values of capacitance increases.
Reason :
When we insert a dielectric between the plates of a capacitor. Potential energy stored in the capacitor decreases
359207
A parallel plate capacitor has plates of area \(A\) separted by distance \(‘d’\) between them. It is filled with a dielectric which has a dielectric constant that varies as \(k\left( x \right) = K\left( {1 + \alpha x} \right)\) where \(‘x’\) is the distance measured from one of the plates. If \(\left( {\alpha d} \right) < < 1\), the total capacitance of the system is best given by the expression :
359209
Assertion :
A parallel plate capacitor is charged to a potential difference of \(100\;V\), and disconnected from the voltage source. A slab of dielectric is then slowly inserted between the plates. Then values of capacitance increases.
Reason :
When we insert a dielectric between the plates of a capacitor. Potential energy stored in the capacitor decreases
359207
A parallel plate capacitor has plates of area \(A\) separted by distance \(‘d’\) between them. It is filled with a dielectric which has a dielectric constant that varies as \(k\left( x \right) = K\left( {1 + \alpha x} \right)\) where \(‘x’\) is the distance measured from one of the plates. If \(\left( {\alpha d} \right) < < 1\), the total capacitance of the system is best given by the expression :
359209
Assertion :
A parallel plate capacitor is charged to a potential difference of \(100\;V\), and disconnected from the voltage source. A slab of dielectric is then slowly inserted between the plates. Then values of capacitance increases.
Reason :
When we insert a dielectric between the plates of a capacitor. Potential energy stored in the capacitor decreases
359207
A parallel plate capacitor has plates of area \(A\) separted by distance \(‘d’\) between them. It is filled with a dielectric which has a dielectric constant that varies as \(k\left( x \right) = K\left( {1 + \alpha x} \right)\) where \(‘x’\) is the distance measured from one of the plates. If \(\left( {\alpha d} \right) < < 1\), the total capacitance of the system is best given by the expression :
359209
Assertion :
A parallel plate capacitor is charged to a potential difference of \(100\;V\), and disconnected from the voltage source. A slab of dielectric is then slowly inserted between the plates. Then values of capacitance increases.
Reason :
When we insert a dielectric between the plates of a capacitor. Potential energy stored in the capacitor decreases
359207
A parallel plate capacitor has plates of area \(A\) separted by distance \(‘d’\) between them. It is filled with a dielectric which has a dielectric constant that varies as \(k\left( x \right) = K\left( {1 + \alpha x} \right)\) where \(‘x’\) is the distance measured from one of the plates. If \(\left( {\alpha d} \right) < < 1\), the total capacitance of the system is best given by the expression :
359209
Assertion :
A parallel plate capacitor is charged to a potential difference of \(100\;V\), and disconnected from the voltage source. A slab of dielectric is then slowly inserted between the plates. Then values of capacitance increases.
Reason :
When we insert a dielectric between the plates of a capacitor. Potential energy stored in the capacitor decreases