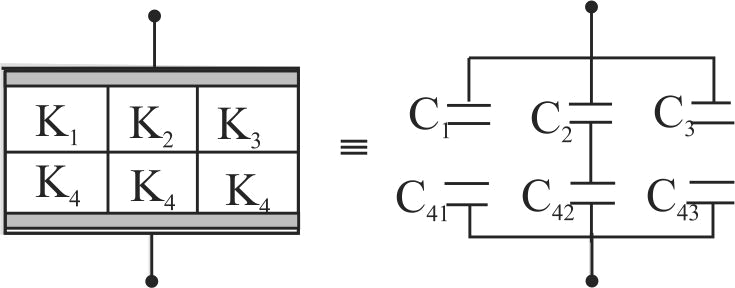
359203 A parallel-plate capacitor of area \(A\), plate separation d and capacitance \(C\) is filled with four dielectric materials having dielectric constants \({K_1},{K_2},{K_3}\,{\mathop{\rm and}\nolimits} \,{K_4}\) as shown in the figure. If a single dielectric material is to be used to have the same capacitance \(C\) in this capacitor, then its dielectric constant \(k\) is given by

359204 A parallel plate condenser is filled with two dielectric as shown. Area of each plate is \(A\) and the separation is \(t\). The dielectric constants are \({k_1}\) and \({k_2}\) respectively. Its capacitance in farad will be

359205 A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (\(U\)) as \(\varepsilon = \alpha U\) where \(\alpha = 2{V^{ - 1}}\). A similar capacitor with no dielectric is charged to \({U_0} = 18V.\) It is then connected to the uncharged capacitor with the dielectric. The final voltage on the capacitors

359206 An uncharged capacitor with a solid dielectric is connecetd to a similar air capacitor charged to a potential of \({V_0}\). If the common potential after sharing of charges becomes \(V\), then the dielectric constant of the solid dielectric must be

359203 A parallel-plate capacitor of area \(A\), plate separation d and capacitance \(C\) is filled with four dielectric materials having dielectric constants \({K_1},{K_2},{K_3}\,{\mathop{\rm and}\nolimits} \,{K_4}\) as shown in the figure. If a single dielectric material is to be used to have the same capacitance \(C\) in this capacitor, then its dielectric constant \(k\) is given by

359204 A parallel plate condenser is filled with two dielectric as shown. Area of each plate is \(A\) and the separation is \(t\). The dielectric constants are \({k_1}\) and \({k_2}\) respectively. Its capacitance in farad will be

359205 A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (\(U\)) as \(\varepsilon = \alpha U\) where \(\alpha = 2{V^{ - 1}}\). A similar capacitor with no dielectric is charged to \({U_0} = 18V.\) It is then connected to the uncharged capacitor with the dielectric. The final voltage on the capacitors

359206 An uncharged capacitor with a solid dielectric is connecetd to a similar air capacitor charged to a potential of \({V_0}\). If the common potential after sharing of charges becomes \(V\), then the dielectric constant of the solid dielectric must be

359203 A parallel-plate capacitor of area \(A\), plate separation d and capacitance \(C\) is filled with four dielectric materials having dielectric constants \({K_1},{K_2},{K_3}\,{\mathop{\rm and}\nolimits} \,{K_4}\) as shown in the figure. If a single dielectric material is to be used to have the same capacitance \(C\) in this capacitor, then its dielectric constant \(k\) is given by

359204 A parallel plate condenser is filled with two dielectric as shown. Area of each plate is \(A\) and the separation is \(t\). The dielectric constants are \({k_1}\) and \({k_2}\) respectively. Its capacitance in farad will be

359205 A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (\(U\)) as \(\varepsilon = \alpha U\) where \(\alpha = 2{V^{ - 1}}\). A similar capacitor with no dielectric is charged to \({U_0} = 18V.\) It is then connected to the uncharged capacitor with the dielectric. The final voltage on the capacitors

359206 An uncharged capacitor with a solid dielectric is connecetd to a similar air capacitor charged to a potential of \({V_0}\). If the common potential after sharing of charges becomes \(V\), then the dielectric constant of the solid dielectric must be

359203 A parallel-plate capacitor of area \(A\), plate separation d and capacitance \(C\) is filled with four dielectric materials having dielectric constants \({K_1},{K_2},{K_3}\,{\mathop{\rm and}\nolimits} \,{K_4}\) as shown in the figure. If a single dielectric material is to be used to have the same capacitance \(C\) in this capacitor, then its dielectric constant \(k\) is given by

359204 A parallel plate condenser is filled with two dielectric as shown. Area of each plate is \(A\) and the separation is \(t\). The dielectric constants are \({k_1}\) and \({k_2}\) respectively. Its capacitance in farad will be

359205 A parallel plate capacitor is filled by a dielectric whose relative permittivity varies with the applied voltage (\(U\)) as \(\varepsilon = \alpha U\) where \(\alpha = 2{V^{ - 1}}\). A similar capacitor with no dielectric is charged to \({U_0} = 18V.\) It is then connected to the uncharged capacitor with the dielectric. The final voltage on the capacitors

359206 An uncharged capacitor with a solid dielectric is connecetd to a similar air capacitor charged to a potential of \({V_0}\). If the common potential after sharing of charges becomes \(V\), then the dielectric constant of the solid dielectric must be