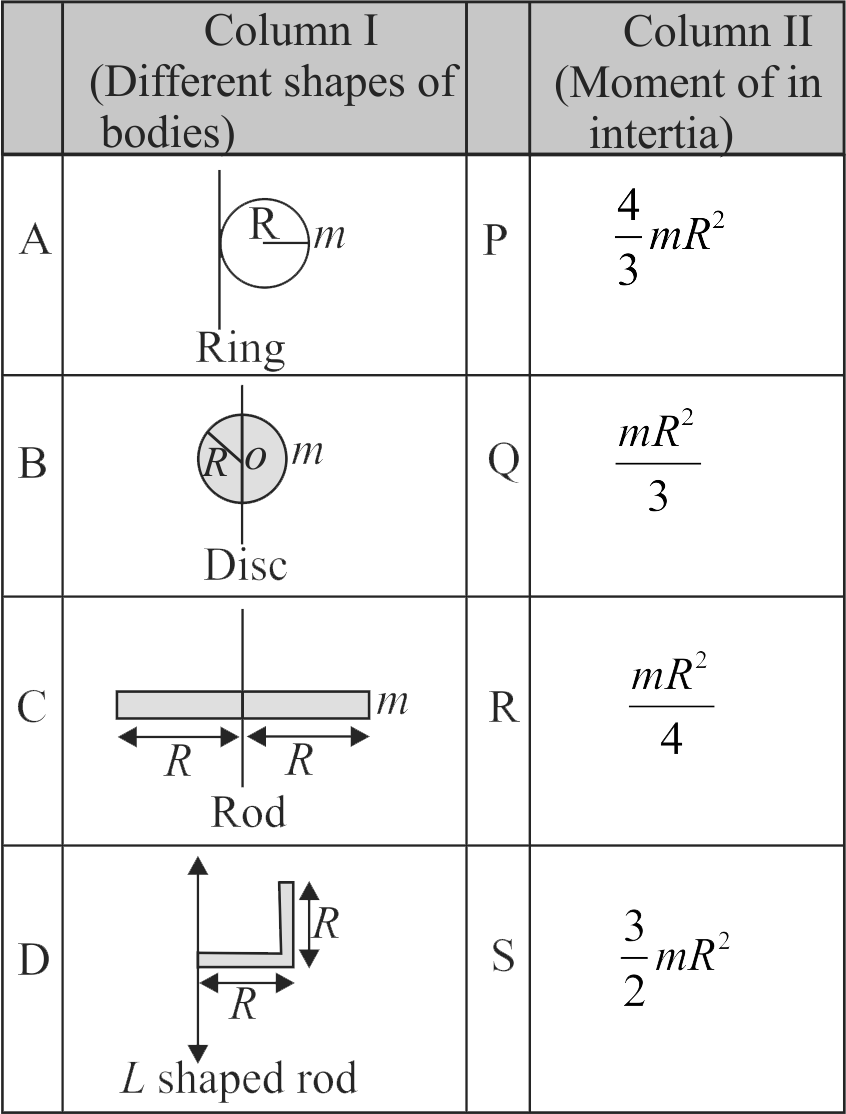
365957
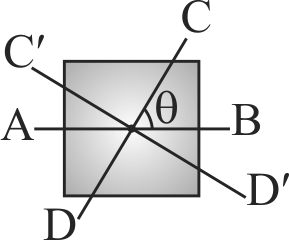
Let \(I\) be the moment of inertia of a uniform square plate about an axis \(\mathrm{AB}\) that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate and it passes through the centre of the plate making an angle \(\theta\) with \(\mathrm{AB}\). The moment of inertia of the plate about the axis \(\mathrm{CD}\) is equal to: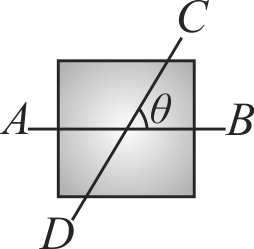
365957
Let \(I\) be the moment of inertia of a uniform square plate about an axis \(\mathrm{AB}\) that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate and it passes through the centre of the plate making an angle \(\theta\) with \(\mathrm{AB}\). The moment of inertia of the plate about the axis \(\mathrm{CD}\) is equal to:
365957
Let \(I\) be the moment of inertia of a uniform square plate about an axis \(\mathrm{AB}\) that passes through its centre and is parallel to two of its sides. CD is a line in the plane of the plate and it passes through the centre of the plate making an angle \(\theta\) with \(\mathrm{AB}\). The moment of inertia of the plate about the axis \(\mathrm{CD}\) is equal to: