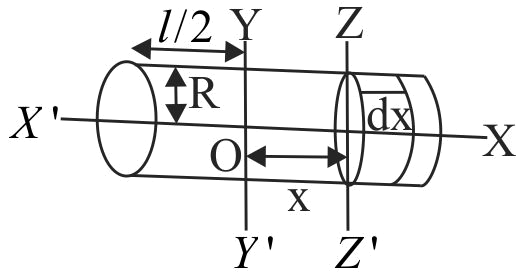
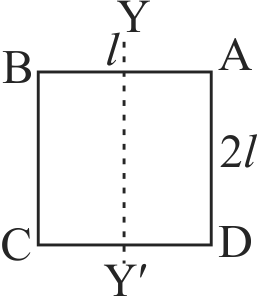
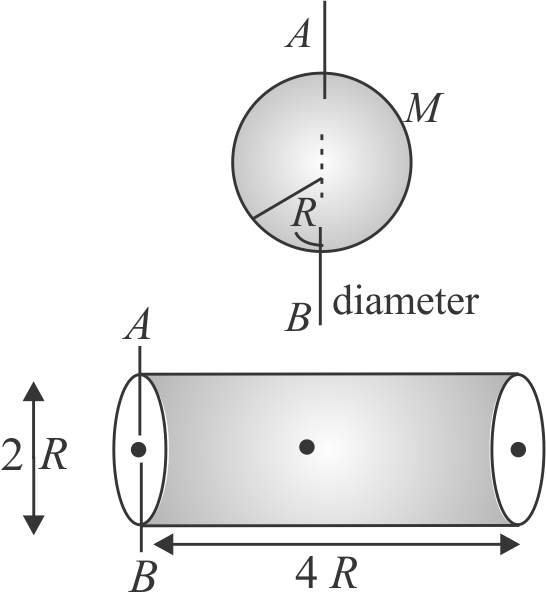
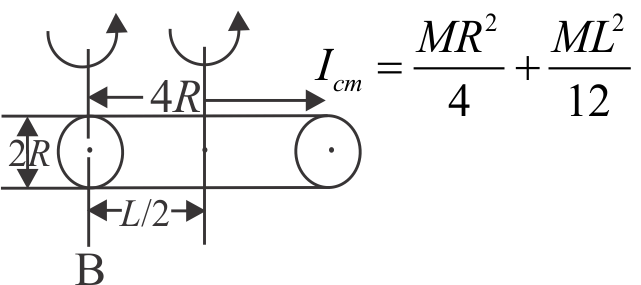
365951 The moment of inertia of a thin uniform rod of mass \(M\) and lenght \(L\) about an axis passing through its mid-point and perpendicular to its length is \(I_{0}\). Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is

365952 A solid cylinder has mass \(M\), radius \(R\) and length \(l\). Its moment of inertia about an axis passing through its centre and perpendicular to its own axis is

365953 The moment of inertia of a sphere of mass \(M\) and radius \(\mathrm{R}\) about an axis passing through its centre is \((2 / 5) M R^{2}\). The radius of gyration of the sphere about a parallel axis to the above and tangent to the sphere is

365954 The moment of inertia of a door of mass \(m\), length \(2 l\) and width \(l\) about its longer side is

365955 Ratio of radius of gyration of a hollow sphere to that of a solid cylinder of equal mass, for moment of inertia about their diameter axis \(A B\) as shown in figure is \(\sqrt{\dfrac{8}{x}}\). The value of \(x\) is

365951 The moment of inertia of a thin uniform rod of mass \(M\) and lenght \(L\) about an axis passing through its mid-point and perpendicular to its length is \(I_{0}\). Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is

365952 A solid cylinder has mass \(M\), radius \(R\) and length \(l\). Its moment of inertia about an axis passing through its centre and perpendicular to its own axis is

365953 The moment of inertia of a sphere of mass \(M\) and radius \(\mathrm{R}\) about an axis passing through its centre is \((2 / 5) M R^{2}\). The radius of gyration of the sphere about a parallel axis to the above and tangent to the sphere is

365954 The moment of inertia of a door of mass \(m\), length \(2 l\) and width \(l\) about its longer side is

365955 Ratio of radius of gyration of a hollow sphere to that of a solid cylinder of equal mass, for moment of inertia about their diameter axis \(A B\) as shown in figure is \(\sqrt{\dfrac{8}{x}}\). The value of \(x\) is

365951 The moment of inertia of a thin uniform rod of mass \(M\) and lenght \(L\) about an axis passing through its mid-point and perpendicular to its length is \(I_{0}\). Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is

365952 A solid cylinder has mass \(M\), radius \(R\) and length \(l\). Its moment of inertia about an axis passing through its centre and perpendicular to its own axis is

365953 The moment of inertia of a sphere of mass \(M\) and radius \(\mathrm{R}\) about an axis passing through its centre is \((2 / 5) M R^{2}\). The radius of gyration of the sphere about a parallel axis to the above and tangent to the sphere is

365954 The moment of inertia of a door of mass \(m\), length \(2 l\) and width \(l\) about its longer side is

365955 Ratio of radius of gyration of a hollow sphere to that of a solid cylinder of equal mass, for moment of inertia about their diameter axis \(A B\) as shown in figure is \(\sqrt{\dfrac{8}{x}}\). The value of \(x\) is

365951 The moment of inertia of a thin uniform rod of mass \(M\) and lenght \(L\) about an axis passing through its mid-point and perpendicular to its length is \(I_{0}\). Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is

365952 A solid cylinder has mass \(M\), radius \(R\) and length \(l\). Its moment of inertia about an axis passing through its centre and perpendicular to its own axis is

365953 The moment of inertia of a sphere of mass \(M\) and radius \(\mathrm{R}\) about an axis passing through its centre is \((2 / 5) M R^{2}\). The radius of gyration of the sphere about a parallel axis to the above and tangent to the sphere is

365954 The moment of inertia of a door of mass \(m\), length \(2 l\) and width \(l\) about its longer side is

365955 Ratio of radius of gyration of a hollow sphere to that of a solid cylinder of equal mass, for moment of inertia about their diameter axis \(A B\) as shown in figure is \(\sqrt{\dfrac{8}{x}}\). The value of \(x\) is

365951 The moment of inertia of a thin uniform rod of mass \(M\) and lenght \(L\) about an axis passing through its mid-point and perpendicular to its length is \(I_{0}\). Its moment of inertia about an axis passing through one of its ends and perpendicular to its length is

365952 A solid cylinder has mass \(M\), radius \(R\) and length \(l\). Its moment of inertia about an axis passing through its centre and perpendicular to its own axis is

365953 The moment of inertia of a sphere of mass \(M\) and radius \(\mathrm{R}\) about an axis passing through its centre is \((2 / 5) M R^{2}\). The radius of gyration of the sphere about a parallel axis to the above and tangent to the sphere is

365954 The moment of inertia of a door of mass \(m\), length \(2 l\) and width \(l\) about its longer side is

365955 Ratio of radius of gyration of a hollow sphere to that of a solid cylinder of equal mass, for moment of inertia about their diameter axis \(A B\) as shown in figure is \(\sqrt{\dfrac{8}{x}}\). The value of \(x\) is