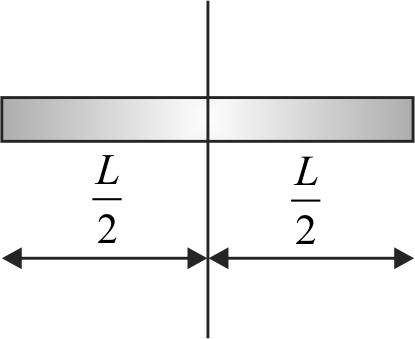365948 A rod of length \(L\) is composed of a uniform length \(\dfrac{1}{2} L\) of wood whose mass is \(m_{w}\) and a uniform length \(\dfrac{1}{2} L\) of brass whose mass is \(m_{b}\). The moment of inertia I of the rod about an axis perpendicular to the rod and through its centre is equal to
365948 A rod of length \(L\) is composed of a uniform length \(\dfrac{1}{2} L\) of wood whose mass is \(m_{w}\) and a uniform length \(\dfrac{1}{2} L\) of brass whose mass is \(m_{b}\). The moment of inertia I of the rod about an axis perpendicular to the rod and through its centre is equal to
365948 A rod of length \(L\) is composed of a uniform length \(\dfrac{1}{2} L\) of wood whose mass is \(m_{w}\) and a uniform length \(\dfrac{1}{2} L\) of brass whose mass is \(m_{b}\). The moment of inertia I of the rod about an axis perpendicular to the rod and through its centre is equal to
365948 A rod of length \(L\) is composed of a uniform length \(\dfrac{1}{2} L\) of wood whose mass is \(m_{w}\) and a uniform length \(\dfrac{1}{2} L\) of brass whose mass is \(m_{b}\). The moment of inertia I of the rod about an axis perpendicular to the rod and through its centre is equal to