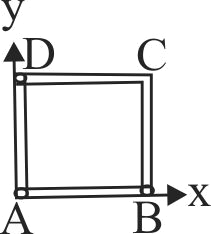
365935 A square frame \(A B C D\) is formed by four identical rods each of mass \(m\) and length \(l\). This frame is in \(x y\) - plane such that side \(AB\) coincides with \(X\) - axis and side \(AD\) along \(Y\) - axis. The moment of inertia of the frame about \(X\) - axis is
365936
Two spheres each of mass \(M\) and radius \(R / 2\) are connected with a mass less rod of length \(2R\) as shown in the figure. The moment of inertia of the system about an axis passing through the centre of one of the spheres and perpendicular to the rod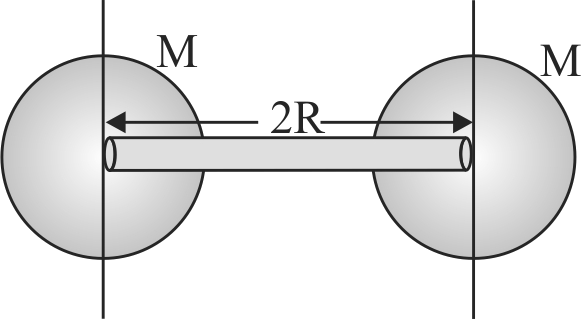
365935 A square frame \(A B C D\) is formed by four identical rods each of mass \(m\) and length \(l\). This frame is in \(x y\) - plane such that side \(AB\) coincides with \(X\) - axis and side \(AD\) along \(Y\) - axis. The moment of inertia of the frame about \(X\) - axis is
365936
Two spheres each of mass \(M\) and radius \(R / 2\) are connected with a mass less rod of length \(2R\) as shown in the figure. The moment of inertia of the system about an axis passing through the centre of one of the spheres and perpendicular to the rod
365935 A square frame \(A B C D\) is formed by four identical rods each of mass \(m\) and length \(l\). This frame is in \(x y\) - plane such that side \(AB\) coincides with \(X\) - axis and side \(AD\) along \(Y\) - axis. The moment of inertia of the frame about \(X\) - axis is
365936
Two spheres each of mass \(M\) and radius \(R / 2\) are connected with a mass less rod of length \(2R\) as shown in the figure. The moment of inertia of the system about an axis passing through the centre of one of the spheres and perpendicular to the rod
365935 A square frame \(A B C D\) is formed by four identical rods each of mass \(m\) and length \(l\). This frame is in \(x y\) - plane such that side \(AB\) coincides with \(X\) - axis and side \(AD\) along \(Y\) - axis. The moment of inertia of the frame about \(X\) - axis is
365936
Two spheres each of mass \(M\) and radius \(R / 2\) are connected with a mass less rod of length \(2R\) as shown in the figure. The moment of inertia of the system about an axis passing through the centre of one of the spheres and perpendicular to the rod