365930
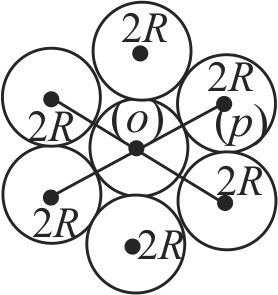
Seven identical circular planar disks, each of mass \(\mathrm{M}\) and radius \(\mathrm{R}\) are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point \(\mathrm{P}\) is: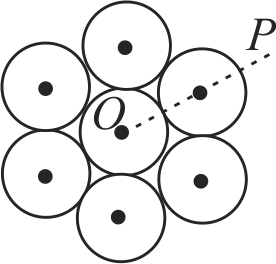
365930
Seven identical circular planar disks, each of mass \(\mathrm{M}\) and radius \(\mathrm{R}\) are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point \(\mathrm{P}\) is:
365930
Seven identical circular planar disks, each of mass \(\mathrm{M}\) and radius \(\mathrm{R}\) are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point \(\mathrm{P}\) is:
365930
Seven identical circular planar disks, each of mass \(\mathrm{M}\) and radius \(\mathrm{R}\) are welded symmetrically as shown. The moment of inertia of the arrangement about the axis normal to the plane and passing through the point \(\mathrm{P}\) is: