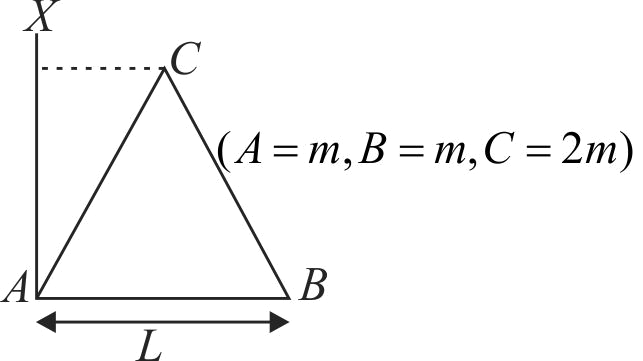365921
Moment of inertia of uniform triangular plate about axis passing through sides \(\mathrm{AB}, \mathrm{AC}\), and \(\mathrm{BC}\) are \(I_{P}, I_{B}\) and \(I_{H}\) respectively and about an axis perpendicular to the plane and passing through point \(\mathrm{C}\) is \(I_{C}\). Then: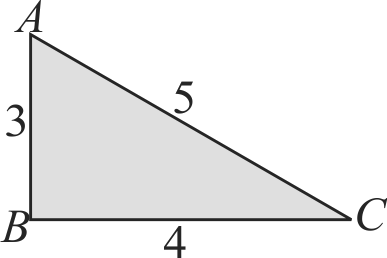
365922 Moment of inertia of a thin uniform rod rotating about the perpendicular axis passing through its centre is \(I\). If the same rod is bent into a ring and its moment of inertia about its diameter is \(I^{\prime}\), then the ratio \(\dfrac{I}{I^{\prime}}\) is
365924
Two particles each mass \(m\), and other particle of mass \(2 m\) are situated at the verticles of an equilateral triangle \(A B C\) of side \(L\). What is the moment of inertia of the system about the line \(A X\) perpendicular to \(A B\) in the plane of \(A B C\) ?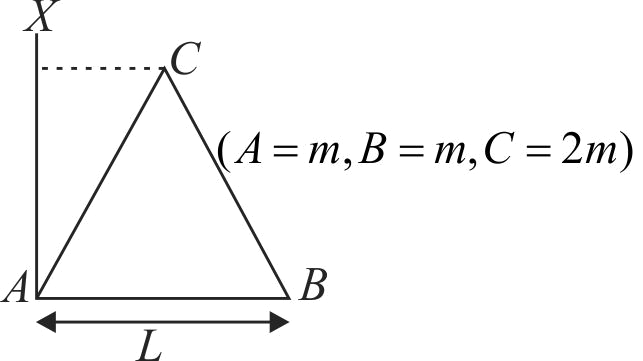
365921
Moment of inertia of uniform triangular plate about axis passing through sides \(\mathrm{AB}, \mathrm{AC}\), and \(\mathrm{BC}\) are \(I_{P}, I_{B}\) and \(I_{H}\) respectively and about an axis perpendicular to the plane and passing through point \(\mathrm{C}\) is \(I_{C}\). Then:
365922 Moment of inertia of a thin uniform rod rotating about the perpendicular axis passing through its centre is \(I\). If the same rod is bent into a ring and its moment of inertia about its diameter is \(I^{\prime}\), then the ratio \(\dfrac{I}{I^{\prime}}\) is
365924
Two particles each mass \(m\), and other particle of mass \(2 m\) are situated at the verticles of an equilateral triangle \(A B C\) of side \(L\). What is the moment of inertia of the system about the line \(A X\) perpendicular to \(A B\) in the plane of \(A B C\) ?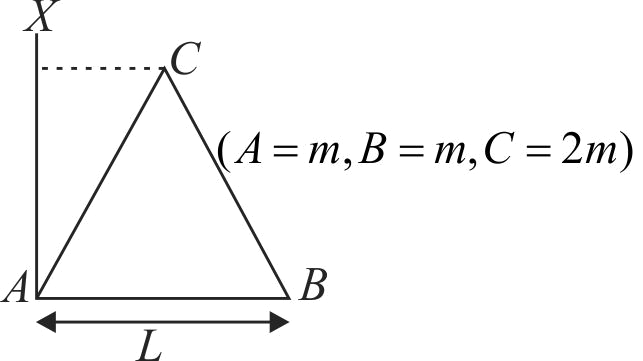
365921
Moment of inertia of uniform triangular plate about axis passing through sides \(\mathrm{AB}, \mathrm{AC}\), and \(\mathrm{BC}\) are \(I_{P}, I_{B}\) and \(I_{H}\) respectively and about an axis perpendicular to the plane and passing through point \(\mathrm{C}\) is \(I_{C}\). Then:
365922 Moment of inertia of a thin uniform rod rotating about the perpendicular axis passing through its centre is \(I\). If the same rod is bent into a ring and its moment of inertia about its diameter is \(I^{\prime}\), then the ratio \(\dfrac{I}{I^{\prime}}\) is
365924
Two particles each mass \(m\), and other particle of mass \(2 m\) are situated at the verticles of an equilateral triangle \(A B C\) of side \(L\). What is the moment of inertia of the system about the line \(A X\) perpendicular to \(A B\) in the plane of \(A B C\) ?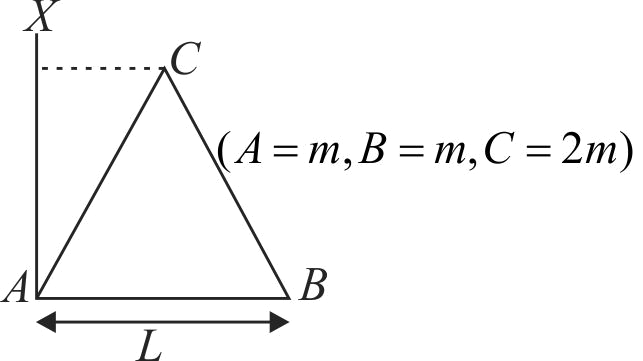
365921
Moment of inertia of uniform triangular plate about axis passing through sides \(\mathrm{AB}, \mathrm{AC}\), and \(\mathrm{BC}\) are \(I_{P}, I_{B}\) and \(I_{H}\) respectively and about an axis perpendicular to the plane and passing through point \(\mathrm{C}\) is \(I_{C}\). Then:
365922 Moment of inertia of a thin uniform rod rotating about the perpendicular axis passing through its centre is \(I\). If the same rod is bent into a ring and its moment of inertia about its diameter is \(I^{\prime}\), then the ratio \(\dfrac{I}{I^{\prime}}\) is
365924
Two particles each mass \(m\), and other particle of mass \(2 m\) are situated at the verticles of an equilateral triangle \(A B C\) of side \(L\). What is the moment of inertia of the system about the line \(A X\) perpendicular to \(A B\) in the plane of \(A B C\) ?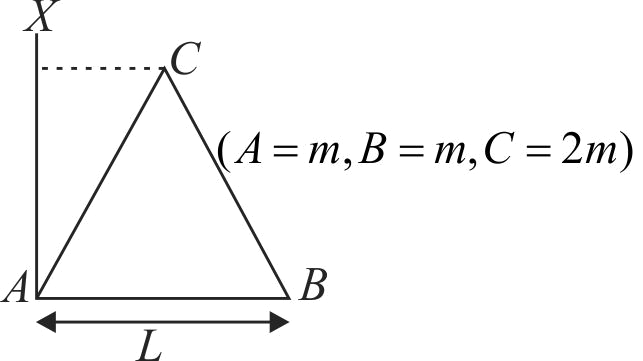
365921
Moment of inertia of uniform triangular plate about axis passing through sides \(\mathrm{AB}, \mathrm{AC}\), and \(\mathrm{BC}\) are \(I_{P}, I_{B}\) and \(I_{H}\) respectively and about an axis perpendicular to the plane and passing through point \(\mathrm{C}\) is \(I_{C}\). Then:
365922 Moment of inertia of a thin uniform rod rotating about the perpendicular axis passing through its centre is \(I\). If the same rod is bent into a ring and its moment of inertia about its diameter is \(I^{\prime}\), then the ratio \(\dfrac{I}{I^{\prime}}\) is
365924
Two particles each mass \(m\), and other particle of mass \(2 m\) are situated at the verticles of an equilateral triangle \(A B C\) of side \(L\). What is the moment of inertia of the system about the line \(A X\) perpendicular to \(A B\) in the plane of \(A B C\) ?