365919
Identify the decreasing order of moment of inertia of the following bodies of same mass and radius
I) about diameter of circular ring
II) about diameter of circular plate
III) about tangent of circular ring \(\perp^{\mathrm{r}}\) to its plane
IV) about tangent of circular plate in its plane
365920
The figure shows a planar body. \(\mathrm{I}_{x}, \mathrm{I}_{\mathrm{y}}\) and \(\mathrm{I}_{\mathrm{z}}\) are moment of inertias of the body about the \(x, \mathrm{y}\) and \(\mathrm{z}\) axes respectively. If \(\mathrm{I}_{\mathrm{z}}=\mathrm{I}_{x}+\mathrm{I}_{\mathrm{y}}\) then predict the correct option.
Theorem of perpendicular axes applicable to a planar body: \(x\) and \(y\) axes are two perpendicular axes in the plane and the \(z\)-axes is perpendicular to the plane.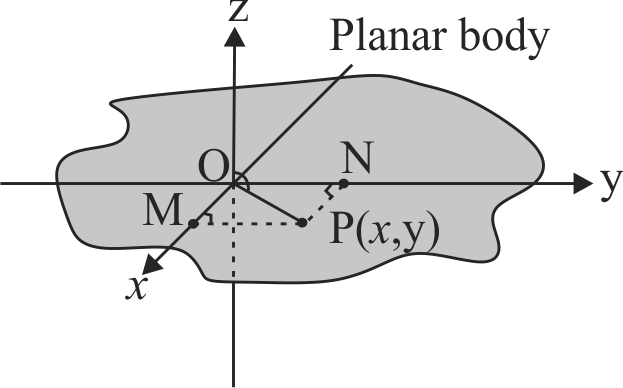
365919
Identify the decreasing order of moment of inertia of the following bodies of same mass and radius
I) about diameter of circular ring
II) about diameter of circular plate
III) about tangent of circular ring \(\perp^{\mathrm{r}}\) to its plane
IV) about tangent of circular plate in its plane
365920
The figure shows a planar body. \(\mathrm{I}_{x}, \mathrm{I}_{\mathrm{y}}\) and \(\mathrm{I}_{\mathrm{z}}\) are moment of inertias of the body about the \(x, \mathrm{y}\) and \(\mathrm{z}\) axes respectively. If \(\mathrm{I}_{\mathrm{z}}=\mathrm{I}_{x}+\mathrm{I}_{\mathrm{y}}\) then predict the correct option.
Theorem of perpendicular axes applicable to a planar body: \(x\) and \(y\) axes are two perpendicular axes in the plane and the \(z\)-axes is perpendicular to the plane.
365919
Identify the decreasing order of moment of inertia of the following bodies of same mass and radius
I) about diameter of circular ring
II) about diameter of circular plate
III) about tangent of circular ring \(\perp^{\mathrm{r}}\) to its plane
IV) about tangent of circular plate in its plane
365920
The figure shows a planar body. \(\mathrm{I}_{x}, \mathrm{I}_{\mathrm{y}}\) and \(\mathrm{I}_{\mathrm{z}}\) are moment of inertias of the body about the \(x, \mathrm{y}\) and \(\mathrm{z}\) axes respectively. If \(\mathrm{I}_{\mathrm{z}}=\mathrm{I}_{x}+\mathrm{I}_{\mathrm{y}}\) then predict the correct option.
Theorem of perpendicular axes applicable to a planar body: \(x\) and \(y\) axes are two perpendicular axes in the plane and the \(z\)-axes is perpendicular to the plane.
365919
Identify the decreasing order of moment of inertia of the following bodies of same mass and radius
I) about diameter of circular ring
II) about diameter of circular plate
III) about tangent of circular ring \(\perp^{\mathrm{r}}\) to its plane
IV) about tangent of circular plate in its plane
365920
The figure shows a planar body. \(\mathrm{I}_{x}, \mathrm{I}_{\mathrm{y}}\) and \(\mathrm{I}_{\mathrm{z}}\) are moment of inertias of the body about the \(x, \mathrm{y}\) and \(\mathrm{z}\) axes respectively. If \(\mathrm{I}_{\mathrm{z}}=\mathrm{I}_{x}+\mathrm{I}_{\mathrm{y}}\) then predict the correct option.
Theorem of perpendicular axes applicable to a planar body: \(x\) and \(y\) axes are two perpendicular axes in the plane and the \(z\)-axes is perpendicular to the plane.