365915
The moment of inertia of a circular disc of radius \(2\;m\) and mass \(1\;kg\) about an axis passing through the centre of mass but perpendicular to the plane of the disc is \(2\;kg\;{m^2}\). Its moment of inertia about an axis parallel to this axis but passing through the edge of the disc is____ (See the given figure).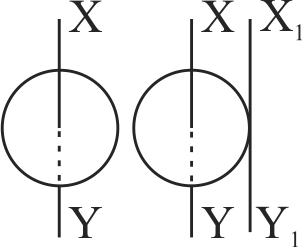
365916
\(A B C\) is right angled triangular plane of uniform thickness. The sides are such that \(A B>B C\) as shown in figure. \(I_{1}, I_{2}, I_{3}\) are moments of inertia about \(A B, B C\) and \(A C\), respectively. Then, which of the following relations is correct?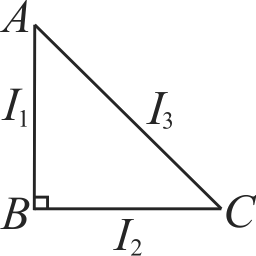
365915
The moment of inertia of a circular disc of radius \(2\;m\) and mass \(1\;kg\) about an axis passing through the centre of mass but perpendicular to the plane of the disc is \(2\;kg\;{m^2}\). Its moment of inertia about an axis parallel to this axis but passing through the edge of the disc is____ (See the given figure).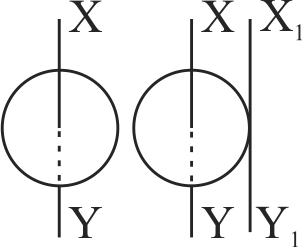
365916
\(A B C\) is right angled triangular plane of uniform thickness. The sides are such that \(A B>B C\) as shown in figure. \(I_{1}, I_{2}, I_{3}\) are moments of inertia about \(A B, B C\) and \(A C\), respectively. Then, which of the following relations is correct?
365915
The moment of inertia of a circular disc of radius \(2\;m\) and mass \(1\;kg\) about an axis passing through the centre of mass but perpendicular to the plane of the disc is \(2\;kg\;{m^2}\). Its moment of inertia about an axis parallel to this axis but passing through the edge of the disc is____ (See the given figure).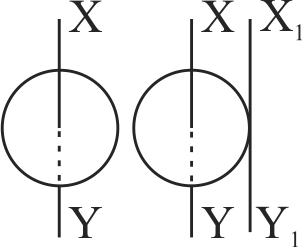
365916
\(A B C\) is right angled triangular plane of uniform thickness. The sides are such that \(A B>B C\) as shown in figure. \(I_{1}, I_{2}, I_{3}\) are moments of inertia about \(A B, B C\) and \(A C\), respectively. Then, which of the following relations is correct?
365915
The moment of inertia of a circular disc of radius \(2\;m\) and mass \(1\;kg\) about an axis passing through the centre of mass but perpendicular to the plane of the disc is \(2\;kg\;{m^2}\). Its moment of inertia about an axis parallel to this axis but passing through the edge of the disc is____ (See the given figure).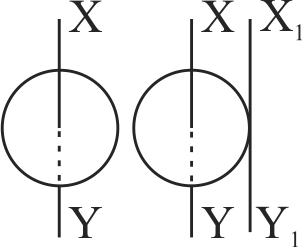
365916
\(A B C\) is right angled triangular plane of uniform thickness. The sides are such that \(A B>B C\) as shown in figure. \(I_{1}, I_{2}, I_{3}\) are moments of inertia about \(A B, B C\) and \(A C\), respectively. Then, which of the following relations is correct?
