365796
A massless spring of force constant \(1000 {Nm}^{-1}\) is compressed a distance of 20 \(cm\) between discs of 8 \(kg\) and 2 \(kg\) , spring is not attached to discs. The system is given an initial velocity \(3 {~ms}^{-1}\) perpendicular to length of spring as shown in the figure. What is ground frame velocity of 2 \(kg\) block when spring regains its natural length.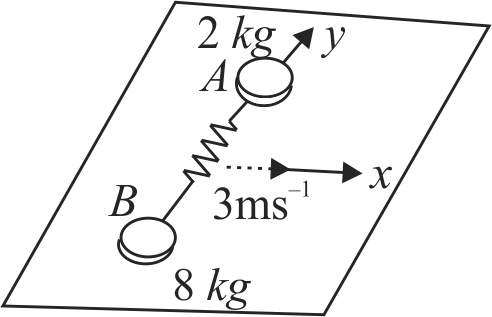
365796
A massless spring of force constant \(1000 {Nm}^{-1}\) is compressed a distance of 20 \(cm\) between discs of 8 \(kg\) and 2 \(kg\) , spring is not attached to discs. The system is given an initial velocity \(3 {~ms}^{-1}\) perpendicular to length of spring as shown in the figure. What is ground frame velocity of 2 \(kg\) block when spring regains its natural length.
365796
A massless spring of force constant \(1000 {Nm}^{-1}\) is compressed a distance of 20 \(cm\) between discs of 8 \(kg\) and 2 \(kg\) , spring is not attached to discs. The system is given an initial velocity \(3 {~ms}^{-1}\) perpendicular to length of spring as shown in the figure. What is ground frame velocity of 2 \(kg\) block when spring regains its natural length.
365796
A massless spring of force constant \(1000 {Nm}^{-1}\) is compressed a distance of 20 \(cm\) between discs of 8 \(kg\) and 2 \(kg\) , spring is not attached to discs. The system is given an initial velocity \(3 {~ms}^{-1}\) perpendicular to length of spring as shown in the figure. What is ground frame velocity of 2 \(kg\) block when spring regains its natural length.
365796
A massless spring of force constant \(1000 {Nm}^{-1}\) is compressed a distance of 20 \(cm\) between discs of 8 \(kg\) and 2 \(kg\) , spring is not attached to discs. The system is given an initial velocity \(3 {~ms}^{-1}\) perpendicular to length of spring as shown in the figure. What is ground frame velocity of 2 \(kg\) block when spring regains its natural length.
