365792 A child is sitting at one end of a long trolley moving with a uniform speed \(v\) on a smooth horizontal track. If the child starts running towards the other end of the trolley with a speed \(u\) (w.r.t trolley), the speed of the centre of mass of the system is
365793
Two balls \(A\) and \(B\) of equal masses are projected upward simultaneously, one from the ground with speed \(50\,\,m{s^{ - 1}}\) and other from height \(40\,m\) above the first ball high tower, with initial speed \(30 {~ms}^{-1}\). Find the maximum height attained by their centre of mass. Take \(g=10 {~m} / {s}^{2}\)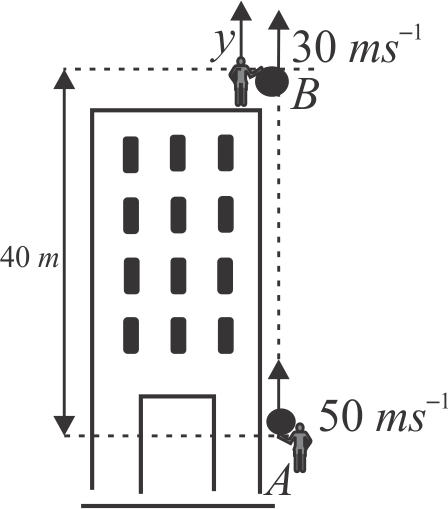
365794
The figure shows a man of mass \(m\) standing at the end \(A\) of a trolley of mass \(M\) placed at rest on a smooth horizontal surface. The man starts moving towards the end \(B\) with a velocity \(u_{r e l}\) with respect to the trolley. The length of the trolley is \(L.\)
When the man starts moving, then the velocity of the trolley with respect to ground will be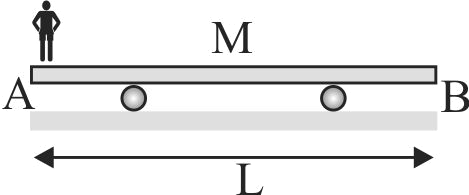
365792 A child is sitting at one end of a long trolley moving with a uniform speed \(v\) on a smooth horizontal track. If the child starts running towards the other end of the trolley with a speed \(u\) (w.r.t trolley), the speed of the centre of mass of the system is
365793
Two balls \(A\) and \(B\) of equal masses are projected upward simultaneously, one from the ground with speed \(50\,\,m{s^{ - 1}}\) and other from height \(40\,m\) above the first ball high tower, with initial speed \(30 {~ms}^{-1}\). Find the maximum height attained by their centre of mass. Take \(g=10 {~m} / {s}^{2}\)
365794
The figure shows a man of mass \(m\) standing at the end \(A\) of a trolley of mass \(M\) placed at rest on a smooth horizontal surface. The man starts moving towards the end \(B\) with a velocity \(u_{r e l}\) with respect to the trolley. The length of the trolley is \(L.\)
When the man starts moving, then the velocity of the trolley with respect to ground will be
365792 A child is sitting at one end of a long trolley moving with a uniform speed \(v\) on a smooth horizontal track. If the child starts running towards the other end of the trolley with a speed \(u\) (w.r.t trolley), the speed of the centre of mass of the system is
365793
Two balls \(A\) and \(B\) of equal masses are projected upward simultaneously, one from the ground with speed \(50\,\,m{s^{ - 1}}\) and other from height \(40\,m\) above the first ball high tower, with initial speed \(30 {~ms}^{-1}\). Find the maximum height attained by their centre of mass. Take \(g=10 {~m} / {s}^{2}\)
365794
The figure shows a man of mass \(m\) standing at the end \(A\) of a trolley of mass \(M\) placed at rest on a smooth horizontal surface. The man starts moving towards the end \(B\) with a velocity \(u_{r e l}\) with respect to the trolley. The length of the trolley is \(L.\)
When the man starts moving, then the velocity of the trolley with respect to ground will be
365792 A child is sitting at one end of a long trolley moving with a uniform speed \(v\) on a smooth horizontal track. If the child starts running towards the other end of the trolley with a speed \(u\) (w.r.t trolley), the speed of the centre of mass of the system is
365793
Two balls \(A\) and \(B\) of equal masses are projected upward simultaneously, one from the ground with speed \(50\,\,m{s^{ - 1}}\) and other from height \(40\,m\) above the first ball high tower, with initial speed \(30 {~ms}^{-1}\). Find the maximum height attained by their centre of mass. Take \(g=10 {~m} / {s}^{2}\)
365794
The figure shows a man of mass \(m\) standing at the end \(A\) of a trolley of mass \(M\) placed at rest on a smooth horizontal surface. The man starts moving towards the end \(B\) with a velocity \(u_{r e l}\) with respect to the trolley. The length of the trolley is \(L.\)
When the man starts moving, then the velocity of the trolley with respect to ground will be
