365749
A circular plate of uniform thickness has a diameter of \(112\;cm.\) A circular portion of diameter \(84\;cm\) is removed from one edge as shown in the figure. The distance of centre of mass of the remaining portion from the centre of plate will be
365751
Three identical spheres, each of mass \(1\;kg\) are kept as shown in figure, touching each other, with their centres on a straight line. If their centres are marked \(P,{\rm{ }}Q,{\rm{ }}R\) respectively, the distance of centre of mass of the system from \(P\) is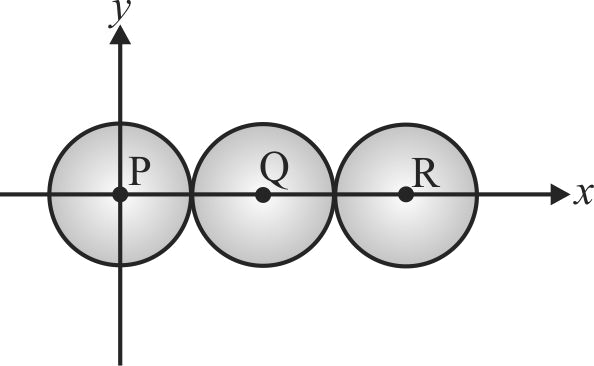
365752
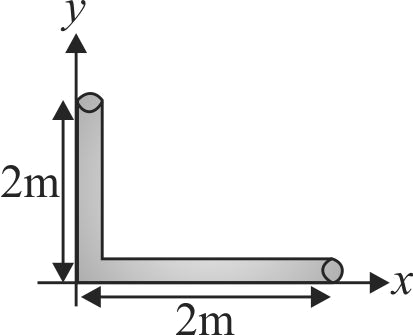
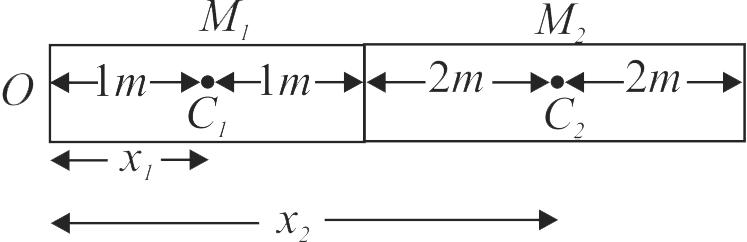
Two uniform rods of different materials \({M_{1}}\) and \({M_{2}}\) have lengths \({2 m}\) and \({4 m}\), respectively. The mass per unit length of rods \({M_{1}}\) and \({M_{2}}\) are \({1 {~kg} / {m}}\) and \({2 {~kg} / {m}}\), respectively. If the rods are arranged, as shown, the position of the centre of mass relative to \({O}\) point is
365749
A circular plate of uniform thickness has a diameter of \(112\;cm.\) A circular portion of diameter \(84\;cm\) is removed from one edge as shown in the figure. The distance of centre of mass of the remaining portion from the centre of plate will be
365751
Three identical spheres, each of mass \(1\;kg\) are kept as shown in figure, touching each other, with their centres on a straight line. If their centres are marked \(P,{\rm{ }}Q,{\rm{ }}R\) respectively, the distance of centre of mass of the system from \(P\) is
365752
Two uniform rods of different materials \({M_{1}}\) and \({M_{2}}\) have lengths \({2 m}\) and \({4 m}\), respectively. The mass per unit length of rods \({M_{1}}\) and \({M_{2}}\) are \({1 {~kg} / {m}}\) and \({2 {~kg} / {m}}\), respectively. If the rods are arranged, as shown, the position of the centre of mass relative to \({O}\) point is
365749
A circular plate of uniform thickness has a diameter of \(112\;cm.\) A circular portion of diameter \(84\;cm\) is removed from one edge as shown in the figure. The distance of centre of mass of the remaining portion from the centre of plate will be
365751
Three identical spheres, each of mass \(1\;kg\) are kept as shown in figure, touching each other, with their centres on a straight line. If their centres are marked \(P,{\rm{ }}Q,{\rm{ }}R\) respectively, the distance of centre of mass of the system from \(P\) is
365752
Two uniform rods of different materials \({M_{1}}\) and \({M_{2}}\) have lengths \({2 m}\) and \({4 m}\), respectively. The mass per unit length of rods \({M_{1}}\) and \({M_{2}}\) are \({1 {~kg} / {m}}\) and \({2 {~kg} / {m}}\), respectively. If the rods are arranged, as shown, the position of the centre of mass relative to \({O}\) point is
365749
A circular plate of uniform thickness has a diameter of \(112\;cm.\) A circular portion of diameter \(84\;cm\) is removed from one edge as shown in the figure. The distance of centre of mass of the remaining portion from the centre of plate will be
365751
Three identical spheres, each of mass \(1\;kg\) are kept as shown in figure, touching each other, with their centres on a straight line. If their centres are marked \(P,{\rm{ }}Q,{\rm{ }}R\) respectively, the distance of centre of mass of the system from \(P\) is
365752
Two uniform rods of different materials \({M_{1}}\) and \({M_{2}}\) have lengths \({2 m}\) and \({4 m}\), respectively. The mass per unit length of rods \({M_{1}}\) and \({M_{2}}\) are \({1 {~kg} / {m}}\) and \({2 {~kg} / {m}}\), respectively. If the rods are arranged, as shown, the position of the centre of mass relative to \({O}\) point is
365749
A circular plate of uniform thickness has a diameter of \(112\;cm.\) A circular portion of diameter \(84\;cm\) is removed from one edge as shown in the figure. The distance of centre of mass of the remaining portion from the centre of plate will be
365751
Three identical spheres, each of mass \(1\;kg\) are kept as shown in figure, touching each other, with their centres on a straight line. If their centres are marked \(P,{\rm{ }}Q,{\rm{ }}R\) respectively, the distance of centre of mass of the system from \(P\) is
365752
Two uniform rods of different materials \({M_{1}}\) and \({M_{2}}\) have lengths \({2 m}\) and \({4 m}\), respectively. The mass per unit length of rods \({M_{1}}\) and \({M_{2}}\) are \({1 {~kg} / {m}}\) and \({2 {~kg} / {m}}\), respectively. If the rods are arranged, as shown, the position of the centre of mass relative to \({O}\) point is