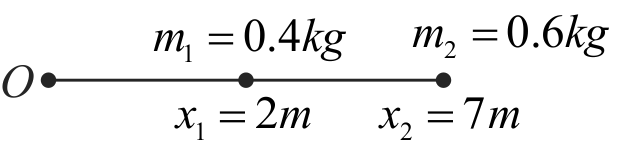
365737 Four particles, each of mass \(1\;kg\) are placed at the corners of a square \(O A B C\) of side \(1\;m\). ' \(O\) ' is at the origin of the coordinate system. \(O A\) and \(O C\) are aligned along positive \(X\)-axis and positive \(Y\)-axis respectively. The position vector of the centre of mass is (in ' \(m\) ')
365737 Four particles, each of mass \(1\;kg\) are placed at the corners of a square \(O A B C\) of side \(1\;m\). ' \(O\) ' is at the origin of the coordinate system. \(O A\) and \(O C\) are aligned along positive \(X\)-axis and positive \(Y\)-axis respectively. The position vector of the centre of mass is (in ' \(m\) ')
365737 Four particles, each of mass \(1\;kg\) are placed at the corners of a square \(O A B C\) of side \(1\;m\). ' \(O\) ' is at the origin of the coordinate system. \(O A\) and \(O C\) are aligned along positive \(X\)-axis and positive \(Y\)-axis respectively. The position vector of the centre of mass is (in ' \(m\) ')
365737 Four particles, each of mass \(1\;kg\) are placed at the corners of a square \(O A B C\) of side \(1\;m\). ' \(O\) ' is at the origin of the coordinate system. \(O A\) and \(O C\) are aligned along positive \(X\)-axis and positive \(Y\)-axis respectively. The position vector of the centre of mass is (in ' \(m\) ')
365737 Four particles, each of mass \(1\;kg\) are placed at the corners of a square \(O A B C\) of side \(1\;m\). ' \(O\) ' is at the origin of the coordinate system. \(O A\) and \(O C\) are aligned along positive \(X\)-axis and positive \(Y\)-axis respectively. The position vector of the centre of mass is (in ' \(m\) ')