365732
Three particles of masses \(1\;kg\), \(\frac{3}{2}\;kg\), and \(2\;kg\) are located at the vertices of an equilateral triangle of side \(a\). Here \(1\;kg\) is placed at origin and \(\dfrac{3}{2} k g\) on the \(x\)-axis. The \(x, y\) coordinates of the centre of mass are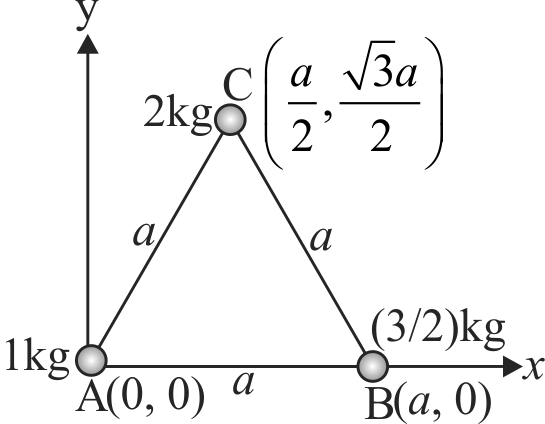
365735 The centre of mass of a system of three particles of masses \(1\;g\), \(2\;g\), and \(3\;g\) is taken as the origin of a coordinate system. The position vector of a fourth particle of mass \(4\;g\) such that the centre of mass of the four particle system lies at the point \((1,2,3)\) is \(\alpha(\hat{i}+2 \hat{j}+3 \hat{k})\), where \(\alpha\) is a constant. The value of \(\alpha\) is
365732
Three particles of masses \(1\;kg\), \(\frac{3}{2}\;kg\), and \(2\;kg\) are located at the vertices of an equilateral triangle of side \(a\). Here \(1\;kg\) is placed at origin and \(\dfrac{3}{2} k g\) on the \(x\)-axis. The \(x, y\) coordinates of the centre of mass are
365735 The centre of mass of a system of three particles of masses \(1\;g\), \(2\;g\), and \(3\;g\) is taken as the origin of a coordinate system. The position vector of a fourth particle of mass \(4\;g\) such that the centre of mass of the four particle system lies at the point \((1,2,3)\) is \(\alpha(\hat{i}+2 \hat{j}+3 \hat{k})\), where \(\alpha\) is a constant. The value of \(\alpha\) is
365732
Three particles of masses \(1\;kg\), \(\frac{3}{2}\;kg\), and \(2\;kg\) are located at the vertices of an equilateral triangle of side \(a\). Here \(1\;kg\) is placed at origin and \(\dfrac{3}{2} k g\) on the \(x\)-axis. The \(x, y\) coordinates of the centre of mass are
365735 The centre of mass of a system of three particles of masses \(1\;g\), \(2\;g\), and \(3\;g\) is taken as the origin of a coordinate system. The position vector of a fourth particle of mass \(4\;g\) such that the centre of mass of the four particle system lies at the point \((1,2,3)\) is \(\alpha(\hat{i}+2 \hat{j}+3 \hat{k})\), where \(\alpha\) is a constant. The value of \(\alpha\) is
365732
Three particles of masses \(1\;kg\), \(\frac{3}{2}\;kg\), and \(2\;kg\) are located at the vertices of an equilateral triangle of side \(a\). Here \(1\;kg\) is placed at origin and \(\dfrac{3}{2} k g\) on the \(x\)-axis. The \(x, y\) coordinates of the centre of mass are
365735 The centre of mass of a system of three particles of masses \(1\;g\), \(2\;g\), and \(3\;g\) is taken as the origin of a coordinate system. The position vector of a fourth particle of mass \(4\;g\) such that the centre of mass of the four particle system lies at the point \((1,2,3)\) is \(\alpha(\hat{i}+2 \hat{j}+3 \hat{k})\), where \(\alpha\) is a constant. The value of \(\alpha\) is
