365728 Four particles of mass \({m_{1}=3 m, m_{2}=4 m}\) \({m_{3}=3 m}\), and \({m_{4}}\) are placed at four corners of a square. What should be the value of \({m_{4}}\) so that the centre of mass of all the four particles are exactly at the centre of the square?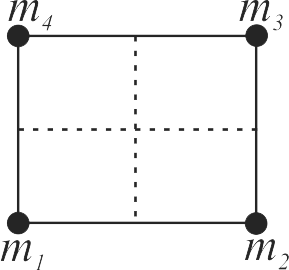

365729 Consider a two particle system with particles having masses \(m_{1}\) and \(m_{2}\). If the first particle is pushed towards the centre of mass through a distance \(d\), by what distance should the second particle be moved, so as to keep the centre of mass at the same position?

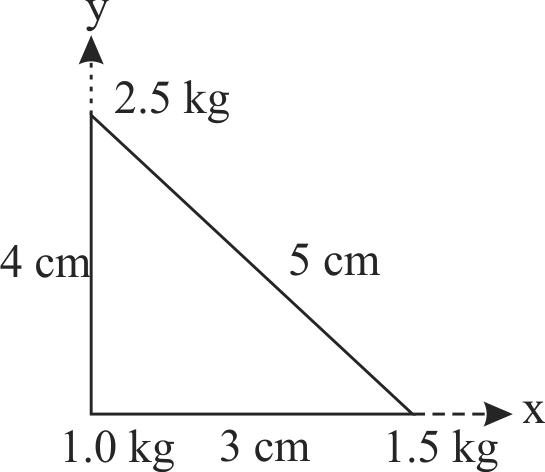
365730 Three point particles of masses \(1.0 \mathrm{~kg}, 1.5 \mathrm{~kg}\) and \(2.5 \mathrm{~kg}\) are placed at three corners of a right angle triangle of sides \(4.0 \mathrm{~cm}, 3.0 \mathrm{~cm}\) and 5.0 \(\mathrm{cm}\) as shown in the figure. The center of mass of the system is at a point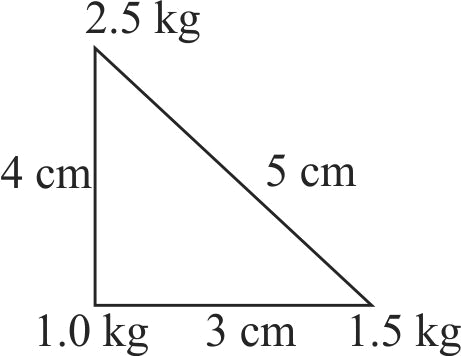

365731 Three particles each of mass \(2\;kg\) are at the corners of an equilateral triangle of side \(\sqrt 3 \;m\). If the one of the particles is removed, the shift in the centre of mass is

365728 Four particles of mass \({m_{1}=3 m, m_{2}=4 m}\) \({m_{3}=3 m}\), and \({m_{4}}\) are placed at four corners of a square. What should be the value of \({m_{4}}\) so that the centre of mass of all the four particles are exactly at the centre of the square?

365729 Consider a two particle system with particles having masses \(m_{1}\) and \(m_{2}\). If the first particle is pushed towards the centre of mass through a distance \(d\), by what distance should the second particle be moved, so as to keep the centre of mass at the same position?

365730 Three point particles of masses \(1.0 \mathrm{~kg}, 1.5 \mathrm{~kg}\) and \(2.5 \mathrm{~kg}\) are placed at three corners of a right angle triangle of sides \(4.0 \mathrm{~cm}, 3.0 \mathrm{~cm}\) and 5.0 \(\mathrm{cm}\) as shown in the figure. The center of mass of the system is at a point

365731 Three particles each of mass \(2\;kg\) are at the corners of an equilateral triangle of side \(\sqrt 3 \;m\). If the one of the particles is removed, the shift in the centre of mass is

365728 Four particles of mass \({m_{1}=3 m, m_{2}=4 m}\) \({m_{3}=3 m}\), and \({m_{4}}\) are placed at four corners of a square. What should be the value of \({m_{4}}\) so that the centre of mass of all the four particles are exactly at the centre of the square?

365729 Consider a two particle system with particles having masses \(m_{1}\) and \(m_{2}\). If the first particle is pushed towards the centre of mass through a distance \(d\), by what distance should the second particle be moved, so as to keep the centre of mass at the same position?

365730 Three point particles of masses \(1.0 \mathrm{~kg}, 1.5 \mathrm{~kg}\) and \(2.5 \mathrm{~kg}\) are placed at three corners of a right angle triangle of sides \(4.0 \mathrm{~cm}, 3.0 \mathrm{~cm}\) and 5.0 \(\mathrm{cm}\) as shown in the figure. The center of mass of the system is at a point

365731 Three particles each of mass \(2\;kg\) are at the corners of an equilateral triangle of side \(\sqrt 3 \;m\). If the one of the particles is removed, the shift in the centre of mass is

365728 Four particles of mass \({m_{1}=3 m, m_{2}=4 m}\) \({m_{3}=3 m}\), and \({m_{4}}\) are placed at four corners of a square. What should be the value of \({m_{4}}\) so that the centre of mass of all the four particles are exactly at the centre of the square?

365729 Consider a two particle system with particles having masses \(m_{1}\) and \(m_{2}\). If the first particle is pushed towards the centre of mass through a distance \(d\), by what distance should the second particle be moved, so as to keep the centre of mass at the same position?

365730 Three point particles of masses \(1.0 \mathrm{~kg}, 1.5 \mathrm{~kg}\) and \(2.5 \mathrm{~kg}\) are placed at three corners of a right angle triangle of sides \(4.0 \mathrm{~cm}, 3.0 \mathrm{~cm}\) and 5.0 \(\mathrm{cm}\) as shown in the figure. The center of mass of the system is at a point

365731 Three particles each of mass \(2\;kg\) are at the corners of an equilateral triangle of side \(\sqrt 3 \;m\). If the one of the particles is removed, the shift in the centre of mass is