365697 A uniform disc of mass \(m\) and radius \(R\) is rotating with angular velocity \(\omega\) on a smooth horizontal surface. Another identical disc is moving translationally with velocity \(v\) as shown.
When they touch each other, they stick together. The angular velocity of centre of mass of the system after contact will be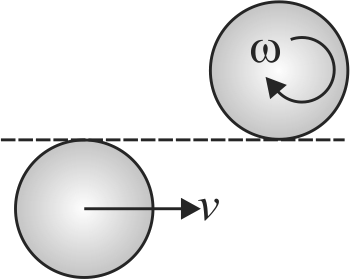

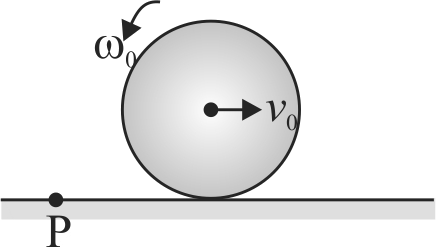
365698 A uniform circular disc of radius \(r\) is placed on a rough horizontal surface and given a linear velocity \(v_{0}\) and angular velocity \(\omega_{0}\) as shown in the figure. The disc comes to rest after moving some distance to the right. It follows that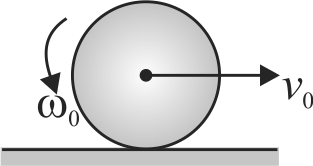

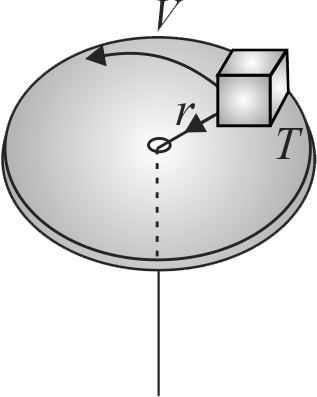
365699 A small block of mass \(3\;kg\) is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius \(0.5\;m\) about the hole with a tangential velocity of \(6\;m{\rm{/}}s.\) The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is \(1000\;N.\) What will be the radius of the circle when the cord breaks?

365700 A small block of mass \(4\,kg\) is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius \(0.5\,m\) about the hole, with a tangential velocity of \({4 {~m} / {s}}\). The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is \(600\,N\). What will be the radius of the circle when the cord breaks?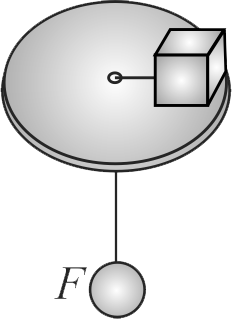

365697 A uniform disc of mass \(m\) and radius \(R\) is rotating with angular velocity \(\omega\) on a smooth horizontal surface. Another identical disc is moving translationally with velocity \(v\) as shown.
When they touch each other, they stick together. The angular velocity of centre of mass of the system after contact will be

365698 A uniform circular disc of radius \(r\) is placed on a rough horizontal surface and given a linear velocity \(v_{0}\) and angular velocity \(\omega_{0}\) as shown in the figure. The disc comes to rest after moving some distance to the right. It follows that

365699 A small block of mass \(3\;kg\) is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius \(0.5\;m\) about the hole with a tangential velocity of \(6\;m{\rm{/}}s.\) The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is \(1000\;N.\) What will be the radius of the circle when the cord breaks?

365700 A small block of mass \(4\,kg\) is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius \(0.5\,m\) about the hole, with a tangential velocity of \({4 {~m} / {s}}\). The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is \(600\,N\). What will be the radius of the circle when the cord breaks?

365697 A uniform disc of mass \(m\) and radius \(R\) is rotating with angular velocity \(\omega\) on a smooth horizontal surface. Another identical disc is moving translationally with velocity \(v\) as shown.
When they touch each other, they stick together. The angular velocity of centre of mass of the system after contact will be

365698 A uniform circular disc of radius \(r\) is placed on a rough horizontal surface and given a linear velocity \(v_{0}\) and angular velocity \(\omega_{0}\) as shown in the figure. The disc comes to rest after moving some distance to the right. It follows that

365699 A small block of mass \(3\;kg\) is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius \(0.5\;m\) about the hole with a tangential velocity of \(6\;m{\rm{/}}s.\) The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is \(1000\;N.\) What will be the radius of the circle when the cord breaks?

365700 A small block of mass \(4\,kg\) is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius \(0.5\,m\) about the hole, with a tangential velocity of \({4 {~m} / {s}}\). The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is \(600\,N\). What will be the radius of the circle when the cord breaks?

365697 A uniform disc of mass \(m\) and radius \(R\) is rotating with angular velocity \(\omega\) on a smooth horizontal surface. Another identical disc is moving translationally with velocity \(v\) as shown.
When they touch each other, they stick together. The angular velocity of centre of mass of the system after contact will be

365698 A uniform circular disc of radius \(r\) is placed on a rough horizontal surface and given a linear velocity \(v_{0}\) and angular velocity \(\omega_{0}\) as shown in the figure. The disc comes to rest after moving some distance to the right. It follows that

365699 A small block of mass \(3\;kg\) is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius \(0.5\;m\) about the hole with a tangential velocity of \(6\;m{\rm{/}}s.\) The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is \(1000\;N.\) What will be the radius of the circle when the cord breaks?

365700 A small block of mass \(4\,kg\) is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius \(0.5\,m\) about the hole, with a tangential velocity of \({4 {~m} / {s}}\). The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is \(600\,N\). What will be the radius of the circle when the cord breaks?