365693 A simplified bola consists of two (instead of the usual three) small but heavy balls connected to a common point by identical lengths of string. To launch it, you hold one of the balls overhead and swing the other ball in a horizontal circle about your wrist. You then let go of the bola which very soon starts rotating around its centre of mass, as shown below. Which one of the following statements holds true when the rotation axis changes from (1) to (2)?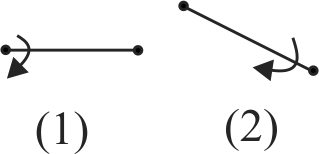

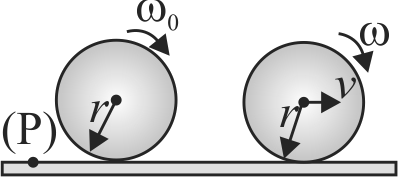
365694 A solid sphere of mass \(M\) and radius \(r\) slips on a rough horizontal surface. At some instant, it has translational velocity \(v_{0}\) and angular velocity \(\omega\left(=\dfrac{v_{0}}{2 \mathrm{r}}\right)\) about its centre as shown in figure. The translational velocity after the sphere starts pure rolling motion is

365695 A hoop of radius \(r\) and mass \(m\) rotating with an angular velocity \(\omega_{0}\) is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip?

365696 A cubical block of side \(30 \mathrm{~cm}\) is moving with velocity \(2 \mathrm{~ms}^{-1}\) on a smooth horizontal surface. The surface has a bump at a point \(\mathrm{O}\) as shown in figure. The angular velocity (in \(\mathrm{rad} / \mathrm{s}\) ) of the block immediately after it hits the bump, is :

365693 A simplified bola consists of two (instead of the usual three) small but heavy balls connected to a common point by identical lengths of string. To launch it, you hold one of the balls overhead and swing the other ball in a horizontal circle about your wrist. You then let go of the bola which very soon starts rotating around its centre of mass, as shown below. Which one of the following statements holds true when the rotation axis changes from (1) to (2)?

365694 A solid sphere of mass \(M\) and radius \(r\) slips on a rough horizontal surface. At some instant, it has translational velocity \(v_{0}\) and angular velocity \(\omega\left(=\dfrac{v_{0}}{2 \mathrm{r}}\right)\) about its centre as shown in figure. The translational velocity after the sphere starts pure rolling motion is

365695 A hoop of radius \(r\) and mass \(m\) rotating with an angular velocity \(\omega_{0}\) is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip?

365696 A cubical block of side \(30 \mathrm{~cm}\) is moving with velocity \(2 \mathrm{~ms}^{-1}\) on a smooth horizontal surface. The surface has a bump at a point \(\mathrm{O}\) as shown in figure. The angular velocity (in \(\mathrm{rad} / \mathrm{s}\) ) of the block immediately after it hits the bump, is :

365693 A simplified bola consists of two (instead of the usual three) small but heavy balls connected to a common point by identical lengths of string. To launch it, you hold one of the balls overhead and swing the other ball in a horizontal circle about your wrist. You then let go of the bola which very soon starts rotating around its centre of mass, as shown below. Which one of the following statements holds true when the rotation axis changes from (1) to (2)?

365694 A solid sphere of mass \(M\) and radius \(r\) slips on a rough horizontal surface. At some instant, it has translational velocity \(v_{0}\) and angular velocity \(\omega\left(=\dfrac{v_{0}}{2 \mathrm{r}}\right)\) about its centre as shown in figure. The translational velocity after the sphere starts pure rolling motion is

365695 A hoop of radius \(r\) and mass \(m\) rotating with an angular velocity \(\omega_{0}\) is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip?

365696 A cubical block of side \(30 \mathrm{~cm}\) is moving with velocity \(2 \mathrm{~ms}^{-1}\) on a smooth horizontal surface. The surface has a bump at a point \(\mathrm{O}\) as shown in figure. The angular velocity (in \(\mathrm{rad} / \mathrm{s}\) ) of the block immediately after it hits the bump, is :

365693 A simplified bola consists of two (instead of the usual three) small but heavy balls connected to a common point by identical lengths of string. To launch it, you hold one of the balls overhead and swing the other ball in a horizontal circle about your wrist. You then let go of the bola which very soon starts rotating around its centre of mass, as shown below. Which one of the following statements holds true when the rotation axis changes from (1) to (2)?

365694 A solid sphere of mass \(M\) and radius \(r\) slips on a rough horizontal surface. At some instant, it has translational velocity \(v_{0}\) and angular velocity \(\omega\left(=\dfrac{v_{0}}{2 \mathrm{r}}\right)\) about its centre as shown in figure. The translational velocity after the sphere starts pure rolling motion is

365695 A hoop of radius \(r\) and mass \(m\) rotating with an angular velocity \(\omega_{0}\) is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it ceases to slip?

365696 A cubical block of side \(30 \mathrm{~cm}\) is moving with velocity \(2 \mathrm{~ms}^{-1}\) on a smooth horizontal surface. The surface has a bump at a point \(\mathrm{O}\) as shown in figure. The angular velocity (in \(\mathrm{rad} / \mathrm{s}\) ) of the block immediately after it hits the bump, is :