365654 A horizontal platform is rotating with uniform angular velocity around the vertical axis passing through its centre. At some instant of time a viscous fluid of mass \(m\) is dropped at the centre and is allowed to spread out and finally falls from the disc. The angular velocity during this period:
365655
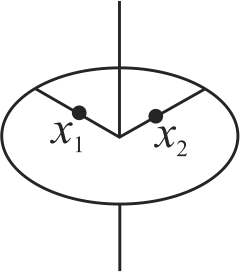
A ring of mass \(M\) and radius \(R\) is rotating with angular speed \(\omega\) about a fixed vertical axis passing through its centre \(\mathrm{O}\) with two point masses each of mass \(\dfrac{M}{8}\) at rest at \(\mathrm{O}\). These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is \(\dfrac{8}{9} \omega\) and one of the masses is at a distance of \(\dfrac{3}{5} R\) from O. At this instant the distance of the other mass from \(\mathrm{O}\) is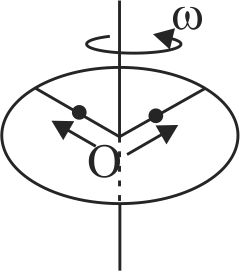
365656 A girl of mass \(M\) stands on the rim of a frictionless merry-go-round of radius \(R\) and rotational inertia \(I\) that is not moving. She throws a rock of mass \(m\) horizontally in a direction that is tangent to the outer edge of the merry-go-round. The speed of the rock, relative to the ground, is \(v\), afterwards the linear speed of the girl is
365657 A man stands on a rotating platform with his arms stretched holding a \(5\;kg\) weight in each hand. The angular speed of the platform is 1.2 rev \({s^{ - 1}}\). The moment of inertia of the man together with the platform may be taken to be constant and equal to \(6\;kg\;{m^2}\). If the man brings his arms close to his chest with the distance of each weight from the axis changing from \(100\,cm\) to \(20\;cm\). The new angular speed of the platform is
365654 A horizontal platform is rotating with uniform angular velocity around the vertical axis passing through its centre. At some instant of time a viscous fluid of mass \(m\) is dropped at the centre and is allowed to spread out and finally falls from the disc. The angular velocity during this period:
365655
A ring of mass \(M\) and radius \(R\) is rotating with angular speed \(\omega\) about a fixed vertical axis passing through its centre \(\mathrm{O}\) with two point masses each of mass \(\dfrac{M}{8}\) at rest at \(\mathrm{O}\). These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is \(\dfrac{8}{9} \omega\) and one of the masses is at a distance of \(\dfrac{3}{5} R\) from O. At this instant the distance of the other mass from \(\mathrm{O}\) is
365656 A girl of mass \(M\) stands on the rim of a frictionless merry-go-round of radius \(R\) and rotational inertia \(I\) that is not moving. She throws a rock of mass \(m\) horizontally in a direction that is tangent to the outer edge of the merry-go-round. The speed of the rock, relative to the ground, is \(v\), afterwards the linear speed of the girl is
365657 A man stands on a rotating platform with his arms stretched holding a \(5\;kg\) weight in each hand. The angular speed of the platform is 1.2 rev \({s^{ - 1}}\). The moment of inertia of the man together with the platform may be taken to be constant and equal to \(6\;kg\;{m^2}\). If the man brings his arms close to his chest with the distance of each weight from the axis changing from \(100\,cm\) to \(20\;cm\). The new angular speed of the platform is
365654 A horizontal platform is rotating with uniform angular velocity around the vertical axis passing through its centre. At some instant of time a viscous fluid of mass \(m\) is dropped at the centre and is allowed to spread out and finally falls from the disc. The angular velocity during this period:
365655
A ring of mass \(M\) and radius \(R\) is rotating with angular speed \(\omega\) about a fixed vertical axis passing through its centre \(\mathrm{O}\) with two point masses each of mass \(\dfrac{M}{8}\) at rest at \(\mathrm{O}\). These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is \(\dfrac{8}{9} \omega\) and one of the masses is at a distance of \(\dfrac{3}{5} R\) from O. At this instant the distance of the other mass from \(\mathrm{O}\) is
365656 A girl of mass \(M\) stands on the rim of a frictionless merry-go-round of radius \(R\) and rotational inertia \(I\) that is not moving. She throws a rock of mass \(m\) horizontally in a direction that is tangent to the outer edge of the merry-go-round. The speed of the rock, relative to the ground, is \(v\), afterwards the linear speed of the girl is
365657 A man stands on a rotating platform with his arms stretched holding a \(5\;kg\) weight in each hand. The angular speed of the platform is 1.2 rev \({s^{ - 1}}\). The moment of inertia of the man together with the platform may be taken to be constant and equal to \(6\;kg\;{m^2}\). If the man brings his arms close to his chest with the distance of each weight from the axis changing from \(100\,cm\) to \(20\;cm\). The new angular speed of the platform is
365654 A horizontal platform is rotating with uniform angular velocity around the vertical axis passing through its centre. At some instant of time a viscous fluid of mass \(m\) is dropped at the centre and is allowed to spread out and finally falls from the disc. The angular velocity during this period:
365655
A ring of mass \(M\) and radius \(R\) is rotating with angular speed \(\omega\) about a fixed vertical axis passing through its centre \(\mathrm{O}\) with two point masses each of mass \(\dfrac{M}{8}\) at rest at \(\mathrm{O}\). These masses can move radially outwards along two massless rods fixed on the ring as shown in the figure. At some instant the angular speed of the system is \(\dfrac{8}{9} \omega\) and one of the masses is at a distance of \(\dfrac{3}{5} R\) from O. At this instant the distance of the other mass from \(\mathrm{O}\) is
365656 A girl of mass \(M\) stands on the rim of a frictionless merry-go-round of radius \(R\) and rotational inertia \(I\) that is not moving. She throws a rock of mass \(m\) horizontally in a direction that is tangent to the outer edge of the merry-go-round. The speed of the rock, relative to the ground, is \(v\), afterwards the linear speed of the girl is
365657 A man stands on a rotating platform with his arms stretched holding a \(5\;kg\) weight in each hand. The angular speed of the platform is 1.2 rev \({s^{ - 1}}\). The moment of inertia of the man together with the platform may be taken to be constant and equal to \(6\;kg\;{m^2}\). If the man brings his arms close to his chest with the distance of each weight from the axis changing from \(100\,cm\) to \(20\;cm\). The new angular speed of the platform is