364833 In an experiment to measure focal length \((f)\) of convex lens, the least counts of the measuring scales for the position of object \((u)\) and for the position of image ( \(v\) ) are \(\Delta u\) and \(\Delta v\), respectively. The error in the measurement of the focal length of the convex lens will be
364836
The following figure shows a beam of light converging at point \(P\). When a concave lens of focal length \(16\;cm\) is introduced in the path of the beam at a place shown by dotted line such that \(OP\) becomes the axis of the lens, the beam converges at a distance \(x\) from the lens.The value of \(x\) will be equal to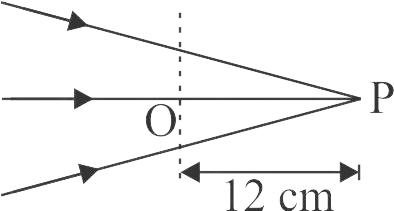
364833 In an experiment to measure focal length \((f)\) of convex lens, the least counts of the measuring scales for the position of object \((u)\) and for the position of image ( \(v\) ) are \(\Delta u\) and \(\Delta v\), respectively. The error in the measurement of the focal length of the convex lens will be
364836
The following figure shows a beam of light converging at point \(P\). When a concave lens of focal length \(16\;cm\) is introduced in the path of the beam at a place shown by dotted line such that \(OP\) becomes the axis of the lens, the beam converges at a distance \(x\) from the lens.The value of \(x\) will be equal to
364833 In an experiment to measure focal length \((f)\) of convex lens, the least counts of the measuring scales for the position of object \((u)\) and for the position of image ( \(v\) ) are \(\Delta u\) and \(\Delta v\), respectively. The error in the measurement of the focal length of the convex lens will be
364836
The following figure shows a beam of light converging at point \(P\). When a concave lens of focal length \(16\;cm\) is introduced in the path of the beam at a place shown by dotted line such that \(OP\) becomes the axis of the lens, the beam converges at a distance \(x\) from the lens.The value of \(x\) will be equal to
364833 In an experiment to measure focal length \((f)\) of convex lens, the least counts of the measuring scales for the position of object \((u)\) and for the position of image ( \(v\) ) are \(\Delta u\) and \(\Delta v\), respectively. The error in the measurement of the focal length of the convex lens will be
364836
The following figure shows a beam of light converging at point \(P\). When a concave lens of focal length \(16\;cm\) is introduced in the path of the beam at a place shown by dotted line such that \(OP\) becomes the axis of the lens, the beam converges at a distance \(x\) from the lens.The value of \(x\) will be equal to
364833 In an experiment to measure focal length \((f)\) of convex lens, the least counts of the measuring scales for the position of object \((u)\) and for the position of image ( \(v\) ) are \(\Delta u\) and \(\Delta v\), respectively. The error in the measurement of the focal length of the convex lens will be
364836
The following figure shows a beam of light converging at point \(P\). When a concave lens of focal length \(16\;cm\) is introduced in the path of the beam at a place shown by dotted line such that \(OP\) becomes the axis of the lens, the beam converges at a distance \(x\) from the lens.The value of \(x\) will be equal to
