Explanation:
The simple pendulum at angular amplitude \(\theta_{0}\) is shown in figure.
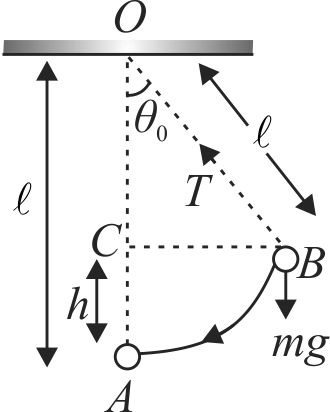
\({T_{\max }} = mg + \frac{{m{v^2}}}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
When bob of the pendulum comes form \(A\) to \(B\), it covers a vertical distance \(h\).
\(\therefore \cos \theta_{0}=\dfrac{l-h}{l}\)
\( \Rightarrow h = l\left( {1 - \cos {\theta _0}} \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
Also, during \(B\) to \(A\), potential energy of bob converts into kinetic energy, i.e., \(m g h=\dfrac{1}{2} m v^{2}\).
\(\therefore v = \sqrt {2gh} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\)
Thus, using Eqs. (1), (2) and (3), we obtain
\(T_{\max }=m g+\dfrac{2 m g}{l}\)
\(\left(1-\cos \theta_{0}\right)\)
\(=m g+2 m g\left[1-1+\dfrac{\theta_{0}^{2}}{2}\right]=m g\left(1+\theta_{0}^{2}\right)\)