364449
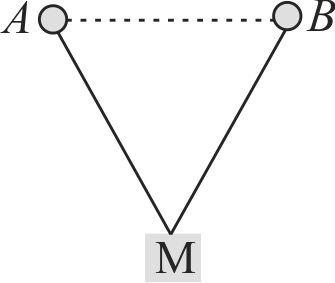
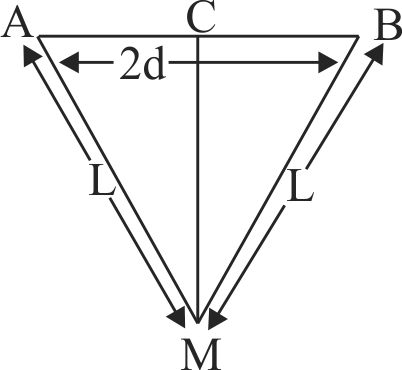
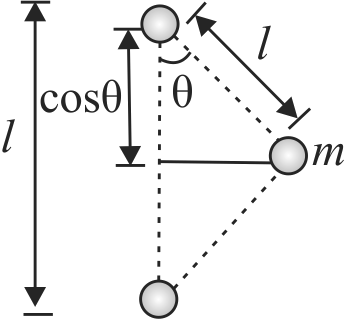
Two light strings, each of length \(l\), are fixed at points \(A\) and \(B\) on a fixed horizontal rod \(xy\). A small bob is tied by both strings the strings are making angle \(45^{\circ}\) with the rod. If the bob is slightly displaced normal to the plane of the strings and released then period of the resulting small oscillation will be: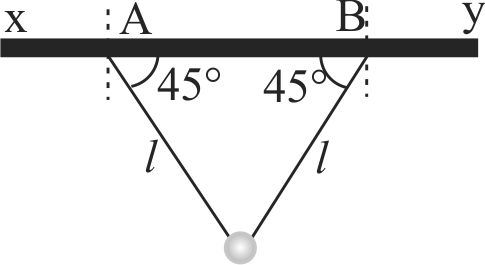
364449
Two light strings, each of length \(l\), are fixed at points \(A\) and \(B\) on a fixed horizontal rod \(xy\). A small bob is tied by both strings the strings are making angle \(45^{\circ}\) with the rod. If the bob is slightly displaced normal to the plane of the strings and released then period of the resulting small oscillation will be:
364449
Two light strings, each of length \(l\), are fixed at points \(A\) and \(B\) on a fixed horizontal rod \(xy\). A small bob is tied by both strings the strings are making angle \(45^{\circ}\) with the rod. If the bob is slightly displaced normal to the plane of the strings and released then period of the resulting small oscillation will be:
364449
Two light strings, each of length \(l\), are fixed at points \(A\) and \(B\) on a fixed horizontal rod \(xy\). A small bob is tied by both strings the strings are making angle \(45^{\circ}\) with the rod. If the bob is slightly displaced normal to the plane of the strings and released then period of the resulting small oscillation will be:
364449
Two light strings, each of length \(l\), are fixed at points \(A\) and \(B\) on a fixed horizontal rod \(xy\). A small bob is tied by both strings the strings are making angle \(45^{\circ}\) with the rod. If the bob is slightly displaced normal to the plane of the strings and released then period of the resulting small oscillation will be: