364424 Two bodies of masses \(1\;kg\) and \(5\;kg\) are connected to a vertical spring (as shown in figure). The smaller mass executes SHM of angular frequency \(16\,rad/s\), and amplitude \(2\;cm\) while the bigger mass remains stationary on the ground. Find the maximum force exerted by the system on the floor.
(Take \(g = 10\;m{s^{ - 2}}\) )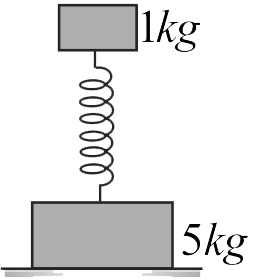

364425 A particle of mass \(m\) connected with a spring of force constant \(k\) is executing SHM with amplitude\(A = 1\;m\). When it is at \( + \frac{A}{2}\) from equilibrium position moving towards right, it receives an impulse which doubles its velocity without changing direction. Its amplitude after the impulse is
(Take \(\sqrt {13} = 3.61\) )

364426
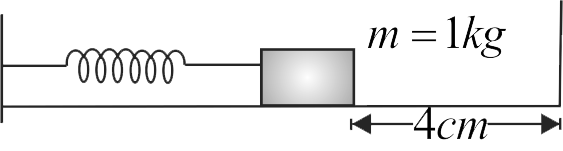
For the arrangement shown in figure, the spring is initially compressed by \(3cm\). When the spring is released the block collides with the wall and rebounds to compress the spring again. The maximum compression in the spring after collision (coefficient of restitution is 0.7) is
(Take \(\sqrt 5 = 2.24,{\mkern 1mu} \,k = {10^4}N/m\))

364427 A mass \(M\), attached to a horizontal spring, executes S.H.M. with amplitude \(A_{1}\). When the mass \(M\) passes through its mean position then a smaller mass \(m\) is placed over it and both of them move together with amplitude \(A_{2}\). The ratio
of \(\left(\dfrac{A_{1}}{A_{2}}\right)\) is:

364424 Two bodies of masses \(1\;kg\) and \(5\;kg\) are connected to a vertical spring (as shown in figure). The smaller mass executes SHM of angular frequency \(16\,rad/s\), and amplitude \(2\;cm\) while the bigger mass remains stationary on the ground. Find the maximum force exerted by the system on the floor.
(Take \(g = 10\;m{s^{ - 2}}\) )

364425 A particle of mass \(m\) connected with a spring of force constant \(k\) is executing SHM with amplitude\(A = 1\;m\). When it is at \( + \frac{A}{2}\) from equilibrium position moving towards right, it receives an impulse which doubles its velocity without changing direction. Its amplitude after the impulse is
(Take \(\sqrt {13} = 3.61\) )

364426
For the arrangement shown in figure, the spring is initially compressed by \(3cm\). When the spring is released the block collides with the wall and rebounds to compress the spring again. The maximum compression in the spring after collision (coefficient of restitution is 0.7) is
(Take \(\sqrt 5 = 2.24,{\mkern 1mu} \,k = {10^4}N/m\))

364427 A mass \(M\), attached to a horizontal spring, executes S.H.M. with amplitude \(A_{1}\). When the mass \(M\) passes through its mean position then a smaller mass \(m\) is placed over it and both of them move together with amplitude \(A_{2}\). The ratio
of \(\left(\dfrac{A_{1}}{A_{2}}\right)\) is:

364424 Two bodies of masses \(1\;kg\) and \(5\;kg\) are connected to a vertical spring (as shown in figure). The smaller mass executes SHM of angular frequency \(16\,rad/s\), and amplitude \(2\;cm\) while the bigger mass remains stationary on the ground. Find the maximum force exerted by the system on the floor.
(Take \(g = 10\;m{s^{ - 2}}\) )

364425 A particle of mass \(m\) connected with a spring of force constant \(k\) is executing SHM with amplitude\(A = 1\;m\). When it is at \( + \frac{A}{2}\) from equilibrium position moving towards right, it receives an impulse which doubles its velocity without changing direction. Its amplitude after the impulse is
(Take \(\sqrt {13} = 3.61\) )

364426
For the arrangement shown in figure, the spring is initially compressed by \(3cm\). When the spring is released the block collides with the wall and rebounds to compress the spring again. The maximum compression in the spring after collision (coefficient of restitution is 0.7) is
(Take \(\sqrt 5 = 2.24,{\mkern 1mu} \,k = {10^4}N/m\))

364427 A mass \(M\), attached to a horizontal spring, executes S.H.M. with amplitude \(A_{1}\). When the mass \(M\) passes through its mean position then a smaller mass \(m\) is placed over it and both of them move together with amplitude \(A_{2}\). The ratio
of \(\left(\dfrac{A_{1}}{A_{2}}\right)\) is:

364424 Two bodies of masses \(1\;kg\) and \(5\;kg\) are connected to a vertical spring (as shown in figure). The smaller mass executes SHM of angular frequency \(16\,rad/s\), and amplitude \(2\;cm\) while the bigger mass remains stationary on the ground. Find the maximum force exerted by the system on the floor.
(Take \(g = 10\;m{s^{ - 2}}\) )

364425 A particle of mass \(m\) connected with a spring of force constant \(k\) is executing SHM with amplitude\(A = 1\;m\). When it is at \( + \frac{A}{2}\) from equilibrium position moving towards right, it receives an impulse which doubles its velocity without changing direction. Its amplitude after the impulse is
(Take \(\sqrt {13} = 3.61\) )

364426
For the arrangement shown in figure, the spring is initially compressed by \(3cm\). When the spring is released the block collides with the wall and rebounds to compress the spring again. The maximum compression in the spring after collision (coefficient of restitution is 0.7) is
(Take \(\sqrt 5 = 2.24,{\mkern 1mu} \,k = {10^4}N/m\))

364427 A mass \(M\), attached to a horizontal spring, executes S.H.M. with amplitude \(A_{1}\). When the mass \(M\) passes through its mean position then a smaller mass \(m\) is placed over it and both of them move together with amplitude \(A_{2}\). The ratio
of \(\left(\dfrac{A_{1}}{A_{2}}\right)\) is: