364430
Two bodies of masses \(1\;kg\) and \(4\;kg\) are connected to a vertical spring, as shown in the figure. The smaller mass executes simple harmonic motion of angular frequency \(25\,rad/s\), and amplitude \(1.6\;cm\) while the bigger mass remains stationary on the ground. The maximum force exerted by the system on the floor is (take \(g = 10\;m{s^{ - 2}}\)).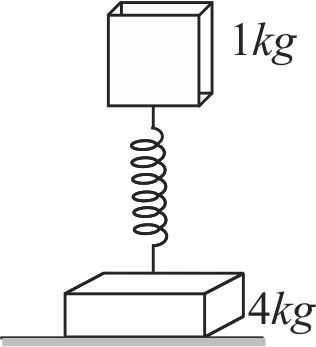
364431
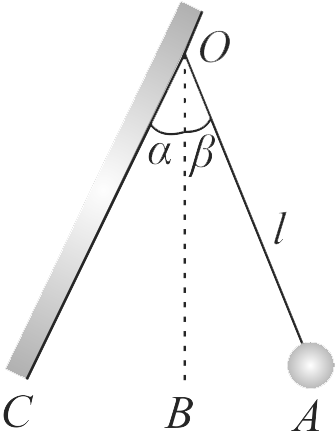
A small ball is suspended by a thread of length \({l=1 {~m}}\) at the point \({O}\) on the wall, forming a small angle \({\alpha=2^{\circ}}\) with the vertical (as shown in figure). Then the thread with ball was deviated through a small angle \({\beta=4^{\circ}}\) and set free. Assuming the collision of the ball against the wall to be perfectly elastic, the oscillation period of such a pendulum is (Take \(g = {\pi ^2}\)).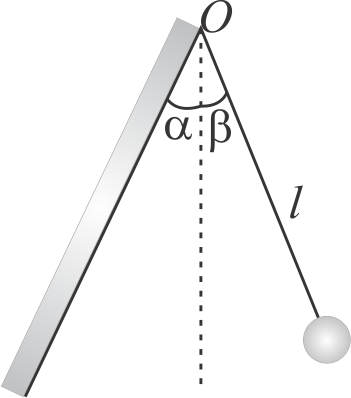
364430
Two bodies of masses \(1\;kg\) and \(4\;kg\) are connected to a vertical spring, as shown in the figure. The smaller mass executes simple harmonic motion of angular frequency \(25\,rad/s\), and amplitude \(1.6\;cm\) while the bigger mass remains stationary on the ground. The maximum force exerted by the system on the floor is (take \(g = 10\;m{s^{ - 2}}\)).
364431
A small ball is suspended by a thread of length \({l=1 {~m}}\) at the point \({O}\) on the wall, forming a small angle \({\alpha=2^{\circ}}\) with the vertical (as shown in figure). Then the thread with ball was deviated through a small angle \({\beta=4^{\circ}}\) and set free. Assuming the collision of the ball against the wall to be perfectly elastic, the oscillation period of such a pendulum is (Take \(g = {\pi ^2}\)).
364430
Two bodies of masses \(1\;kg\) and \(4\;kg\) are connected to a vertical spring, as shown in the figure. The smaller mass executes simple harmonic motion of angular frequency \(25\,rad/s\), and amplitude \(1.6\;cm\) while the bigger mass remains stationary on the ground. The maximum force exerted by the system on the floor is (take \(g = 10\;m{s^{ - 2}}\)).
364431
A small ball is suspended by a thread of length \({l=1 {~m}}\) at the point \({O}\) on the wall, forming a small angle \({\alpha=2^{\circ}}\) with the vertical (as shown in figure). Then the thread with ball was deviated through a small angle \({\beta=4^{\circ}}\) and set free. Assuming the collision of the ball against the wall to be perfectly elastic, the oscillation period of such a pendulum is (Take \(g = {\pi ^2}\)).
364430
Two bodies of masses \(1\;kg\) and \(4\;kg\) are connected to a vertical spring, as shown in the figure. The smaller mass executes simple harmonic motion of angular frequency \(25\,rad/s\), and amplitude \(1.6\;cm\) while the bigger mass remains stationary on the ground. The maximum force exerted by the system on the floor is (take \(g = 10\;m{s^{ - 2}}\)).
364431
A small ball is suspended by a thread of length \({l=1 {~m}}\) at the point \({O}\) on the wall, forming a small angle \({\alpha=2^{\circ}}\) with the vertical (as shown in figure). Then the thread with ball was deviated through a small angle \({\beta=4^{\circ}}\) and set free. Assuming the collision of the ball against the wall to be perfectly elastic, the oscillation period of such a pendulum is (Take \(g = {\pi ^2}\)).
364430
Two bodies of masses \(1\;kg\) and \(4\;kg\) are connected to a vertical spring, as shown in the figure. The smaller mass executes simple harmonic motion of angular frequency \(25\,rad/s\), and amplitude \(1.6\;cm\) while the bigger mass remains stationary on the ground. The maximum force exerted by the system on the floor is (take \(g = 10\;m{s^{ - 2}}\)).
364431
A small ball is suspended by a thread of length \({l=1 {~m}}\) at the point \({O}\) on the wall, forming a small angle \({\alpha=2^{\circ}}\) with the vertical (as shown in figure). Then the thread with ball was deviated through a small angle \({\beta=4^{\circ}}\) and set free. Assuming the collision of the ball against the wall to be perfectly elastic, the oscillation period of such a pendulum is (Take \(g = {\pi ^2}\)).