364421
A mass \(M\) is attached to a horizontal spring of force constant \(k\) fixed on one side to a rigid support as shown figure. The mass oscillates on a frictionless surface with time period \(T\) and amplitude A. When the mass is in equilibrium position, another mass \(m\) is gently placed on it and both stick together. What will be the new amplitude of oscillation?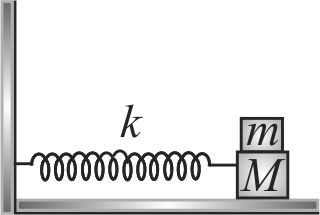
364421
A mass \(M\) is attached to a horizontal spring of force constant \(k\) fixed on one side to a rigid support as shown figure. The mass oscillates on a frictionless surface with time period \(T\) and amplitude A. When the mass is in equilibrium position, another mass \(m\) is gently placed on it and both stick together. What will be the new amplitude of oscillation?
364421
A mass \(M\) is attached to a horizontal spring of force constant \(k\) fixed on one side to a rigid support as shown figure. The mass oscillates on a frictionless surface with time period \(T\) and amplitude A. When the mass is in equilibrium position, another mass \(m\) is gently placed on it and both stick together. What will be the new amplitude of oscillation?
364421
A mass \(M\) is attached to a horizontal spring of force constant \(k\) fixed on one side to a rigid support as shown figure. The mass oscillates on a frictionless surface with time period \(T\) and amplitude A. When the mass is in equilibrium position, another mass \(m\) is gently placed on it and both stick together. What will be the new amplitude of oscillation?