364416 Two bodies \({M}\) and \({N}\) of equal masses are suspended from two separate springs of constants \({k_{1}}\) and \({k_{2}}\) respectively. If \({M}\) and \({N}\) oscillate vertically so that their maximum velocities are equal, the ratio of amplitude of vibration of \({M}\) to that of \({N}\) is
364418
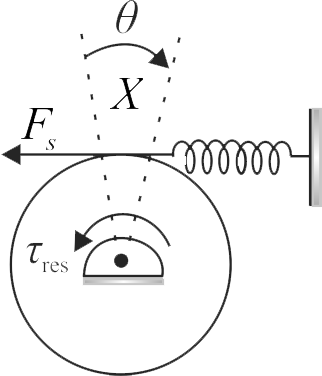
A uniform disc of mass \(m = 2\;kg\) and radius \(R = 5\;cm\) is pivoted smoothly at its centre of mass. A light spring of stiffness \(k\) is attached with the disc tangentially (as shown in figure). Find the angular frequency of torsional oscillation of the disc is
(Take \(k = 5N/s,\sqrt 5 = 2.23)\)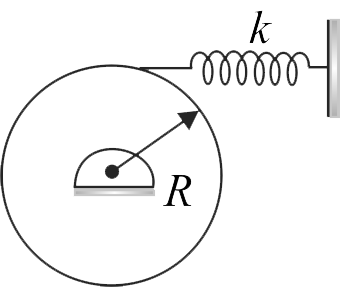
364416 Two bodies \({M}\) and \({N}\) of equal masses are suspended from two separate springs of constants \({k_{1}}\) and \({k_{2}}\) respectively. If \({M}\) and \({N}\) oscillate vertically so that their maximum velocities are equal, the ratio of amplitude of vibration of \({M}\) to that of \({N}\) is
364418
A uniform disc of mass \(m = 2\;kg\) and radius \(R = 5\;cm\) is pivoted smoothly at its centre of mass. A light spring of stiffness \(k\) is attached with the disc tangentially (as shown in figure). Find the angular frequency of torsional oscillation of the disc is
(Take \(k = 5N/s,\sqrt 5 = 2.23)\)
364416 Two bodies \({M}\) and \({N}\) of equal masses are suspended from two separate springs of constants \({k_{1}}\) and \({k_{2}}\) respectively. If \({M}\) and \({N}\) oscillate vertically so that their maximum velocities are equal, the ratio of amplitude of vibration of \({M}\) to that of \({N}\) is
364418
A uniform disc of mass \(m = 2\;kg\) and radius \(R = 5\;cm\) is pivoted smoothly at its centre of mass. A light spring of stiffness \(k\) is attached with the disc tangentially (as shown in figure). Find the angular frequency of torsional oscillation of the disc is
(Take \(k = 5N/s,\sqrt 5 = 2.23)\)
364416 Two bodies \({M}\) and \({N}\) of equal masses are suspended from two separate springs of constants \({k_{1}}\) and \({k_{2}}\) respectively. If \({M}\) and \({N}\) oscillate vertically so that their maximum velocities are equal, the ratio of amplitude of vibration of \({M}\) to that of \({N}\) is
364418
A uniform disc of mass \(m = 2\;kg\) and radius \(R = 5\;cm\) is pivoted smoothly at its centre of mass. A light spring of stiffness \(k\) is attached with the disc tangentially (as shown in figure). Find the angular frequency of torsional oscillation of the disc is
(Take \(k = 5N/s,\sqrt 5 = 2.23)\)
364416 Two bodies \({M}\) and \({N}\) of equal masses are suspended from two separate springs of constants \({k_{1}}\) and \({k_{2}}\) respectively. If \({M}\) and \({N}\) oscillate vertically so that their maximum velocities are equal, the ratio of amplitude of vibration of \({M}\) to that of \({N}\) is
364418
A uniform disc of mass \(m = 2\;kg\) and radius \(R = 5\;cm\) is pivoted smoothly at its centre of mass. A light spring of stiffness \(k\) is attached with the disc tangentially (as shown in figure). Find the angular frequency of torsional oscillation of the disc is
(Take \(k = 5N/s,\sqrt 5 = 2.23)\)