364411
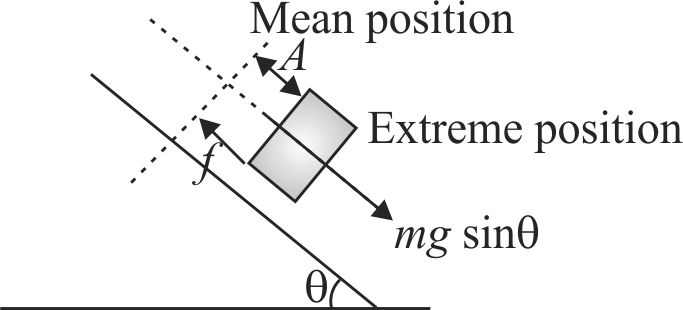
The coefficient of friction between block of mass \(m\) and \(2\;m\) is \(\mu=2 \tan \theta\). There is no friction between block of mass \(2\;m\) and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks is
364413
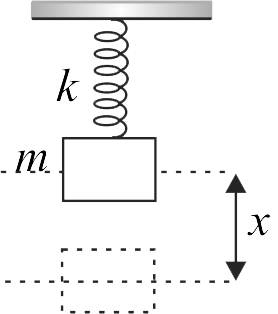
A body of mass \('m'\) is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand, so that the spring is neither stretched nor compressed. Suddenly, the support of the hand is removed. The lowest position attained by the mass during oscillation is \(8\;cm\) below the point, where it was held in hand. The frequency of oscillation is
(Take \(\sqrt {9.8} = \pi \) )
364414 A simple harmonic oscillator consists of a particle of mass \(m\) and an ideal spring with spring constant \(k\). The particle oscillates with a time period \(T\). The spring is cut into two equal parts. If one part oscillates with the same particle, the time period will be
364411
The coefficient of friction between block of mass \(m\) and \(2\;m\) is \(\mu=2 \tan \theta\). There is no friction between block of mass \(2\;m\) and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks is
364413
A body of mass \('m'\) is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand, so that the spring is neither stretched nor compressed. Suddenly, the support of the hand is removed. The lowest position attained by the mass during oscillation is \(8\;cm\) below the point, where it was held in hand. The frequency of oscillation is
(Take \(\sqrt {9.8} = \pi \) )
364414 A simple harmonic oscillator consists of a particle of mass \(m\) and an ideal spring with spring constant \(k\). The particle oscillates with a time period \(T\). The spring is cut into two equal parts. If one part oscillates with the same particle, the time period will be
364411
The coefficient of friction between block of mass \(m\) and \(2\;m\) is \(\mu=2 \tan \theta\). There is no friction between block of mass \(2\;m\) and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks is
364413
A body of mass \('m'\) is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand, so that the spring is neither stretched nor compressed. Suddenly, the support of the hand is removed. The lowest position attained by the mass during oscillation is \(8\;cm\) below the point, where it was held in hand. The frequency of oscillation is
(Take \(\sqrt {9.8} = \pi \) )
364414 A simple harmonic oscillator consists of a particle of mass \(m\) and an ideal spring with spring constant \(k\). The particle oscillates with a time period \(T\). The spring is cut into two equal parts. If one part oscillates with the same particle, the time period will be
364411
The coefficient of friction between block of mass \(m\) and \(2\;m\) is \(\mu=2 \tan \theta\). There is no friction between block of mass \(2\;m\) and inclined plane. The maximum amplitude of the two block system for which there is no relative motion between both the blocks is
364413
A body of mass \('m'\) is attached to one end of a massless spring which is suspended vertically from a fixed point. The mass is held in hand, so that the spring is neither stretched nor compressed. Suddenly, the support of the hand is removed. The lowest position attained by the mass during oscillation is \(8\;cm\) below the point, where it was held in hand. The frequency of oscillation is
(Take \(\sqrt {9.8} = \pi \) )
364414 A simple harmonic oscillator consists of a particle of mass \(m\) and an ideal spring with spring constant \(k\). The particle oscillates with a time period \(T\). The spring is cut into two equal parts. If one part oscillates with the same particle, the time period will be