364407 A mass of \(250\;g\) hangs on a spring and oscillates vertically with a period of \(1.1\;s\). To double the period, what mass must be added to the \(250\;g\) ? (Ignore the mass of the spring)

364408 A block of mass \(m\) rests on a platform. The platform is given up and down SHM with an amplitude \(\mathrm{d}\). What can be the maximum frequency so that the block never leaves the platform?

364409 For a simple harmonic motion in a mass spring system shown, the surface is frictionless. When the mass of the block is \(1\;kg\), the angular

frequency is \({\omega _1}\). When the mass is \(2\;kg\) the angular frequency is \({\omega _2}\). The ratio \({\omega _2}/{\omega _1}\) is

364410 A block of mass \(100\;g\) attached to a spring of spring constant \(100\;N{\rm{/}}m\) is lying on a frictionless floor as shown. The block is moved to compress the spring by \(10\;cm\) and then released. If the collisions with the wall in front are elastic, then the time period of the motion is: (Given \(\pi^{2}=10\) )

364407 A mass of \(250\;g\) hangs on a spring and oscillates vertically with a period of \(1.1\;s\). To double the period, what mass must be added to the \(250\;g\) ? (Ignore the mass of the spring)

364408 A block of mass \(m\) rests on a platform. The platform is given up and down SHM with an amplitude \(\mathrm{d}\). What can be the maximum frequency so that the block never leaves the platform?

364409 For a simple harmonic motion in a mass spring system shown, the surface is frictionless. When the mass of the block is \(1\;kg\), the angular

frequency is \({\omega _1}\). When the mass is \(2\;kg\) the angular frequency is \({\omega _2}\). The ratio \({\omega _2}/{\omega _1}\) is

364410 A block of mass \(100\;g\) attached to a spring of spring constant \(100\;N{\rm{/}}m\) is lying on a frictionless floor as shown. The block is moved to compress the spring by \(10\;cm\) and then released. If the collisions with the wall in front are elastic, then the time period of the motion is: (Given \(\pi^{2}=10\) )

364407 A mass of \(250\;g\) hangs on a spring and oscillates vertically with a period of \(1.1\;s\). To double the period, what mass must be added to the \(250\;g\) ? (Ignore the mass of the spring)

364408 A block of mass \(m\) rests on a platform. The platform is given up and down SHM with an amplitude \(\mathrm{d}\). What can be the maximum frequency so that the block never leaves the platform?

364409 For a simple harmonic motion in a mass spring system shown, the surface is frictionless. When the mass of the block is \(1\;kg\), the angular

frequency is \({\omega _1}\). When the mass is \(2\;kg\) the angular frequency is \({\omega _2}\). The ratio \({\omega _2}/{\omega _1}\) is

364410 A block of mass \(100\;g\) attached to a spring of spring constant \(100\;N{\rm{/}}m\) is lying on a frictionless floor as shown. The block is moved to compress the spring by \(10\;cm\) and then released. If the collisions with the wall in front are elastic, then the time period of the motion is: (Given \(\pi^{2}=10\) )

364407 A mass of \(250\;g\) hangs on a spring and oscillates vertically with a period of \(1.1\;s\). To double the period, what mass must be added to the \(250\;g\) ? (Ignore the mass of the spring)

364408 A block of mass \(m\) rests on a platform. The platform is given up and down SHM with an amplitude \(\mathrm{d}\). What can be the maximum frequency so that the block never leaves the platform?

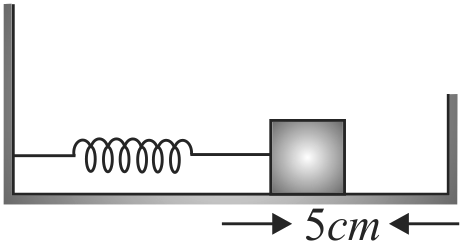
364409 For a simple harmonic motion in a mass spring system shown, the surface is frictionless. When the mass of the block is \(1\;kg\), the angular

frequency is \({\omega _1}\). When the mass is \(2\;kg\) the angular frequency is \({\omega _2}\). The ratio \({\omega _2}/{\omega _1}\) is

364410 A block of mass \(100\;g\) attached to a spring of spring constant \(100\;N{\rm{/}}m\) is lying on a frictionless floor as shown. The block is moved to compress the spring by \(10\;cm\) and then released. If the collisions with the wall in front are elastic, then the time period of the motion is: (Given \(\pi^{2}=10\) )