364403
A horizontal rod of mass \(m\) and length \(L\) is pivoted at one end. The rod's other end is supported by a spring of force constant \(k\). The rod is displaced by a small angle \(\theta\) from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion is
364405 Two bodies \(A\) and \(B\) of equal mass are suspended from two separate massles springs of force constant \(k_{1}\) and \(k_{2}\) respectively. The bodies oscillate vertically such that their maximum velocities are equal. The ratio of the amplitudes of body \(A\) to that of body \(B\) is
364406
A block \(A\) of mass \(m\) is connected to spring and performs simple harmonic motion with a time period of \(2 s\). Another block \(B\) of mass \(m\) rests on \(A\). The coefficient of static friction betwwen \(A\) and \(B\) is \(\mu_{s}=0.6\). The maximum amplitude of oscillation which the system can have so that there is no relative motion between \(A\) and \(B\) is (take \(\pi^{2}=g=10\) )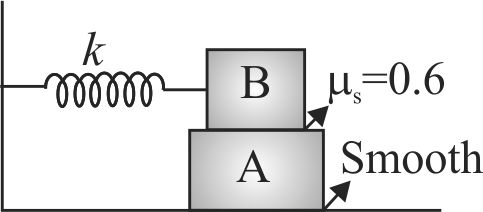
364403
A horizontal rod of mass \(m\) and length \(L\) is pivoted at one end. The rod's other end is supported by a spring of force constant \(k\). The rod is displaced by a small angle \(\theta\) from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion is
364405 Two bodies \(A\) and \(B\) of equal mass are suspended from two separate massles springs of force constant \(k_{1}\) and \(k_{2}\) respectively. The bodies oscillate vertically such that their maximum velocities are equal. The ratio of the amplitudes of body \(A\) to that of body \(B\) is
364406
A block \(A\) of mass \(m\) is connected to spring and performs simple harmonic motion with a time period of \(2 s\). Another block \(B\) of mass \(m\) rests on \(A\). The coefficient of static friction betwwen \(A\) and \(B\) is \(\mu_{s}=0.6\). The maximum amplitude of oscillation which the system can have so that there is no relative motion between \(A\) and \(B\) is (take \(\pi^{2}=g=10\) )
364403
A horizontal rod of mass \(m\) and length \(L\) is pivoted at one end. The rod's other end is supported by a spring of force constant \(k\). The rod is displaced by a small angle \(\theta\) from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion is
364405 Two bodies \(A\) and \(B\) of equal mass are suspended from two separate massles springs of force constant \(k_{1}\) and \(k_{2}\) respectively. The bodies oscillate vertically such that their maximum velocities are equal. The ratio of the amplitudes of body \(A\) to that of body \(B\) is
364406
A block \(A\) of mass \(m\) is connected to spring and performs simple harmonic motion with a time period of \(2 s\). Another block \(B\) of mass \(m\) rests on \(A\). The coefficient of static friction betwwen \(A\) and \(B\) is \(\mu_{s}=0.6\). The maximum amplitude of oscillation which the system can have so that there is no relative motion between \(A\) and \(B\) is (take \(\pi^{2}=g=10\) )
364403
A horizontal rod of mass \(m\) and length \(L\) is pivoted at one end. The rod's other end is supported by a spring of force constant \(k\). The rod is displaced by a small angle \(\theta\) from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion is
364405 Two bodies \(A\) and \(B\) of equal mass are suspended from two separate massles springs of force constant \(k_{1}\) and \(k_{2}\) respectively. The bodies oscillate vertically such that their maximum velocities are equal. The ratio of the amplitudes of body \(A\) to that of body \(B\) is
364406
A block \(A\) of mass \(m\) is connected to spring and performs simple harmonic motion with a time period of \(2 s\). Another block \(B\) of mass \(m\) rests on \(A\). The coefficient of static friction betwwen \(A\) and \(B\) is \(\mu_{s}=0.6\). The maximum amplitude of oscillation which the system can have so that there is no relative motion between \(A\) and \(B\) is (take \(\pi^{2}=g=10\) )

