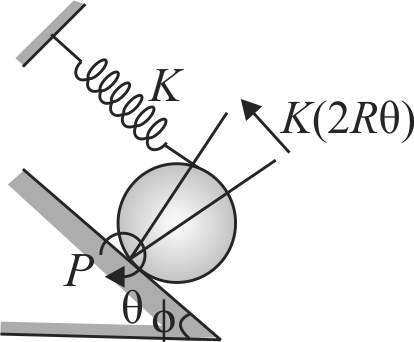
364398
A uniform cylinder of mass \(m=2 {~kg}\) and radius \(R=0.50\) \(m\) is in equilibrium on an inclined plane by the action of a light spring of stiffness \(K=300 {~N} / {m}\), gravity and reaction force acting on it. If the angle of inclination of the plane is \(\phi=30^{\circ}\), find the angular frequency of small oscillation of the cylinder.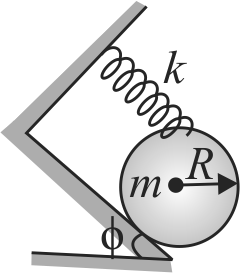
364400
A mass \(m\) is hung on an ideal massless spring. Another equal mass is connected to the other end of the spring. the whole system is at rest. At \(t = 0,\;m\) is released and the system falls freely under gravity. Assume that natural length of the spring is \(L_{0}\), its initial stretched length is \(L\) and the acceleration due to gravity is \(g\). What is distance between masses as function of time?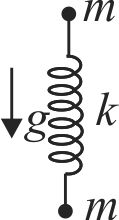
364401 A mass \(m_{1}\) connected to a horizontal spring perform SHM with amplitude \(A\). While mass \(m_{1}\) is passing through mean position, another mass \(m_{2}\) is placed on it so that both the masses move together with amplitude \(A_{1}\). The ratio of \(\dfrac{A_{1}}{A}\) is \(\left(m_{2} < m_{1}\right)\)
364402 A body of mass \(64\;g\) is made to oscillate turn by turn on two different springs \(A\) and \(B\). Spring \(A\) and \(B\) has force constant \(4 \dfrac{N}{m}\) and \(16 \dfrac{N}{m}\) respectively. If \(T_{1}\) and \(T_{2}\) are period of oscillations of spring \(A\) and \(B\) respectively, then \(\dfrac{T_{1}+T_{2}}{T_{1}-T_{2}}\) will be
364398
A uniform cylinder of mass \(m=2 {~kg}\) and radius \(R=0.50\) \(m\) is in equilibrium on an inclined plane by the action of a light spring of stiffness \(K=300 {~N} / {m}\), gravity and reaction force acting on it. If the angle of inclination of the plane is \(\phi=30^{\circ}\), find the angular frequency of small oscillation of the cylinder.
364400
A mass \(m\) is hung on an ideal massless spring. Another equal mass is connected to the other end of the spring. the whole system is at rest. At \(t = 0,\;m\) is released and the system falls freely under gravity. Assume that natural length of the spring is \(L_{0}\), its initial stretched length is \(L\) and the acceleration due to gravity is \(g\). What is distance between masses as function of time?
364401 A mass \(m_{1}\) connected to a horizontal spring perform SHM with amplitude \(A\). While mass \(m_{1}\) is passing through mean position, another mass \(m_{2}\) is placed on it so that both the masses move together with amplitude \(A_{1}\). The ratio of \(\dfrac{A_{1}}{A}\) is \(\left(m_{2} < m_{1}\right)\)
364402 A body of mass \(64\;g\) is made to oscillate turn by turn on two different springs \(A\) and \(B\). Spring \(A\) and \(B\) has force constant \(4 \dfrac{N}{m}\) and \(16 \dfrac{N}{m}\) respectively. If \(T_{1}\) and \(T_{2}\) are period of oscillations of spring \(A\) and \(B\) respectively, then \(\dfrac{T_{1}+T_{2}}{T_{1}-T_{2}}\) will be
364398
A uniform cylinder of mass \(m=2 {~kg}\) and radius \(R=0.50\) \(m\) is in equilibrium on an inclined plane by the action of a light spring of stiffness \(K=300 {~N} / {m}\), gravity and reaction force acting on it. If the angle of inclination of the plane is \(\phi=30^{\circ}\), find the angular frequency of small oscillation of the cylinder.
364400
A mass \(m\) is hung on an ideal massless spring. Another equal mass is connected to the other end of the spring. the whole system is at rest. At \(t = 0,\;m\) is released and the system falls freely under gravity. Assume that natural length of the spring is \(L_{0}\), its initial stretched length is \(L\) and the acceleration due to gravity is \(g\). What is distance between masses as function of time?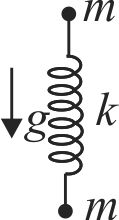
364401 A mass \(m_{1}\) connected to a horizontal spring perform SHM with amplitude \(A\). While mass \(m_{1}\) is passing through mean position, another mass \(m_{2}\) is placed on it so that both the masses move together with amplitude \(A_{1}\). The ratio of \(\dfrac{A_{1}}{A}\) is \(\left(m_{2} < m_{1}\right)\)
364402 A body of mass \(64\;g\) is made to oscillate turn by turn on two different springs \(A\) and \(B\). Spring \(A\) and \(B\) has force constant \(4 \dfrac{N}{m}\) and \(16 \dfrac{N}{m}\) respectively. If \(T_{1}\) and \(T_{2}\) are period of oscillations of spring \(A\) and \(B\) respectively, then \(\dfrac{T_{1}+T_{2}}{T_{1}-T_{2}}\) will be
364398
A uniform cylinder of mass \(m=2 {~kg}\) and radius \(R=0.50\) \(m\) is in equilibrium on an inclined plane by the action of a light spring of stiffness \(K=300 {~N} / {m}\), gravity and reaction force acting on it. If the angle of inclination of the plane is \(\phi=30^{\circ}\), find the angular frequency of small oscillation of the cylinder.
364400
A mass \(m\) is hung on an ideal massless spring. Another equal mass is connected to the other end of the spring. the whole system is at rest. At \(t = 0,\;m\) is released and the system falls freely under gravity. Assume that natural length of the spring is \(L_{0}\), its initial stretched length is \(L\) and the acceleration due to gravity is \(g\). What is distance between masses as function of time?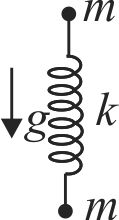
364401 A mass \(m_{1}\) connected to a horizontal spring perform SHM with amplitude \(A\). While mass \(m_{1}\) is passing through mean position, another mass \(m_{2}\) is placed on it so that both the masses move together with amplitude \(A_{1}\). The ratio of \(\dfrac{A_{1}}{A}\) is \(\left(m_{2} < m_{1}\right)\)
364402 A body of mass \(64\;g\) is made to oscillate turn by turn on two different springs \(A\) and \(B\). Spring \(A\) and \(B\) has force constant \(4 \dfrac{N}{m}\) and \(16 \dfrac{N}{m}\) respectively. If \(T_{1}\) and \(T_{2}\) are period of oscillations of spring \(A\) and \(B\) respectively, then \(\dfrac{T_{1}+T_{2}}{T_{1}-T_{2}}\) will be
364398
A uniform cylinder of mass \(m=2 {~kg}\) and radius \(R=0.50\) \(m\) is in equilibrium on an inclined plane by the action of a light spring of stiffness \(K=300 {~N} / {m}\), gravity and reaction force acting on it. If the angle of inclination of the plane is \(\phi=30^{\circ}\), find the angular frequency of small oscillation of the cylinder.
364400
A mass \(m\) is hung on an ideal massless spring. Another equal mass is connected to the other end of the spring. the whole system is at rest. At \(t = 0,\;m\) is released and the system falls freely under gravity. Assume that natural length of the spring is \(L_{0}\), its initial stretched length is \(L\) and the acceleration due to gravity is \(g\). What is distance between masses as function of time?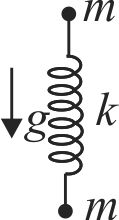
364401 A mass \(m_{1}\) connected to a horizontal spring perform SHM with amplitude \(A\). While mass \(m_{1}\) is passing through mean position, another mass \(m_{2}\) is placed on it so that both the masses move together with amplitude \(A_{1}\). The ratio of \(\dfrac{A_{1}}{A}\) is \(\left(m_{2} < m_{1}\right)\)
364402 A body of mass \(64\;g\) is made to oscillate turn by turn on two different springs \(A\) and \(B\). Spring \(A\) and \(B\) has force constant \(4 \dfrac{N}{m}\) and \(16 \dfrac{N}{m}\) respectively. If \(T_{1}\) and \(T_{2}\) are period of oscillations of spring \(A\) and \(B\) respectively, then \(\dfrac{T_{1}+T_{2}}{T_{1}-T_{2}}\) will be