364396
A uniform rod of length \(l\) and mass \(m = 1\;kg\) is hinged at its lowest point \(\mathrm{O}\) and is connected at its highest point \(A\) by means of a spring of spring constant \(k\) (in fig.). When it is pushed slightly, what is the frequency of oscillation? (Take \(l = 2\;m,k = 10 \,units,{\rm{ }}\sqrt {10} = 3.14\) )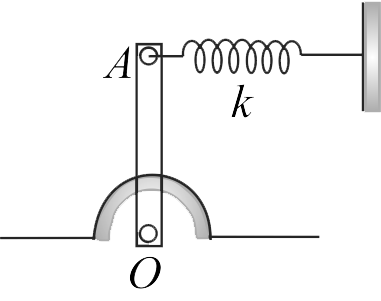
364396
A uniform rod of length \(l\) and mass \(m = 1\;kg\) is hinged at its lowest point \(\mathrm{O}\) and is connected at its highest point \(A\) by means of a spring of spring constant \(k\) (in fig.). When it is pushed slightly, what is the frequency of oscillation? (Take \(l = 2\;m,k = 10 \,units,{\rm{ }}\sqrt {10} = 3.14\) )
364396
A uniform rod of length \(l\) and mass \(m = 1\;kg\) is hinged at its lowest point \(\mathrm{O}\) and is connected at its highest point \(A\) by means of a spring of spring constant \(k\) (in fig.). When it is pushed slightly, what is the frequency of oscillation? (Take \(l = 2\;m,k = 10 \,units,{\rm{ }}\sqrt {10} = 3.14\) )
364396
A uniform rod of length \(l\) and mass \(m = 1\;kg\) is hinged at its lowest point \(\mathrm{O}\) and is connected at its highest point \(A\) by means of a spring of spring constant \(k\) (in fig.). When it is pushed slightly, what is the frequency of oscillation? (Take \(l = 2\;m,k = 10 \,units,{\rm{ }}\sqrt {10} = 3.14\) )

