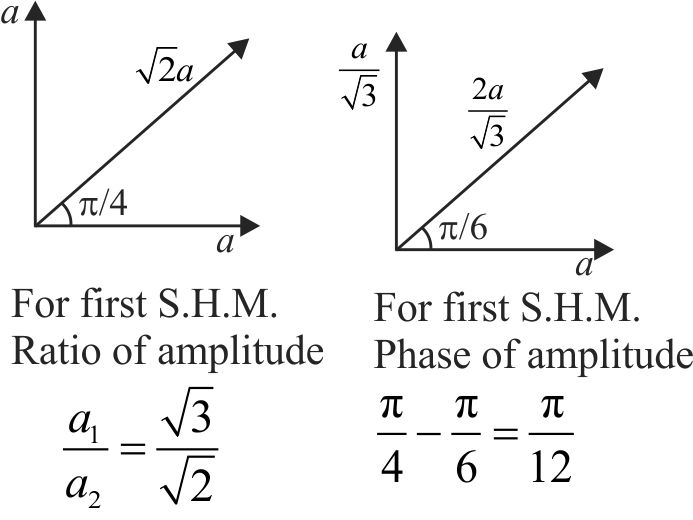
364232 Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is

364233 Two pendulums of length \(121\;cm\) and \(100\;cm\) start vibrating in phase. At some instant, the two are at their mean position in the same phase. The minimum number of vibrations of the shorter pendulum after which the two are again in phase at the mean position is

364234 Two simple harmonic motions are given by \(x_{1}=a \sin \omega t+a \cos \omega t\) and \(x_{2}=a \sin \omega t+\dfrac{a}{\sqrt{3}} \cos \omega t\).
The ratio of the amplitudes of first and second motion and the phase difference between them are respectively

364235 The displacement of a particle along the \(X\) - axis is given by \(x=a \sin ^{2} \omega t\). The motion of the particle corresponds to

364232 Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is

364233 Two pendulums of length \(121\;cm\) and \(100\;cm\) start vibrating in phase. At some instant, the two are at their mean position in the same phase. The minimum number of vibrations of the shorter pendulum after which the two are again in phase at the mean position is

364234 Two simple harmonic motions are given by \(x_{1}=a \sin \omega t+a \cos \omega t\) and \(x_{2}=a \sin \omega t+\dfrac{a}{\sqrt{3}} \cos \omega t\).
The ratio of the amplitudes of first and second motion and the phase difference between them are respectively

364235 The displacement of a particle along the \(X\) - axis is given by \(x=a \sin ^{2} \omega t\). The motion of the particle corresponds to

364232 Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is

364233 Two pendulums of length \(121\;cm\) and \(100\;cm\) start vibrating in phase. At some instant, the two are at their mean position in the same phase. The minimum number of vibrations of the shorter pendulum after which the two are again in phase at the mean position is

364234 Two simple harmonic motions are given by \(x_{1}=a \sin \omega t+a \cos \omega t\) and \(x_{2}=a \sin \omega t+\dfrac{a}{\sqrt{3}} \cos \omega t\).
The ratio of the amplitudes of first and second motion and the phase difference between them are respectively

364235 The displacement of a particle along the \(X\) - axis is given by \(x=a \sin ^{2} \omega t\). The motion of the particle corresponds to

364232 Two particles are oscillating along two close parallel straight lines side by side, with the same frequency and amplitudes. They pass each other, moving in opposite directions when their displacement is half of the amplitude. The mean positions of the two particles lie on a straight line perpendicular to the paths of the two particles. The phase difference is

364233 Two pendulums of length \(121\;cm\) and \(100\;cm\) start vibrating in phase. At some instant, the two are at their mean position in the same phase. The minimum number of vibrations of the shorter pendulum after which the two are again in phase at the mean position is

364234 Two simple harmonic motions are given by \(x_{1}=a \sin \omega t+a \cos \omega t\) and \(x_{2}=a \sin \omega t+\dfrac{a}{\sqrt{3}} \cos \omega t\).
The ratio of the amplitudes of first and second motion and the phase difference between them are respectively

364235 The displacement of a particle along the \(X\) - axis is given by \(x=a \sin ^{2} \omega t\). The motion of the particle corresponds to