358504
There is a horizontal cylindrical uniform but time varying magnetic field increasing at a constant rate \(dB/dt\) as shown in figure. A charged particle having charge \(q\) and mass \(m\) is kept in equilibrium, at the top of a spring of spring constant \(K\), in such a way that it is on the horizontal line passing through the center of the magnetic field as shown in the figure. The compression in the spring will be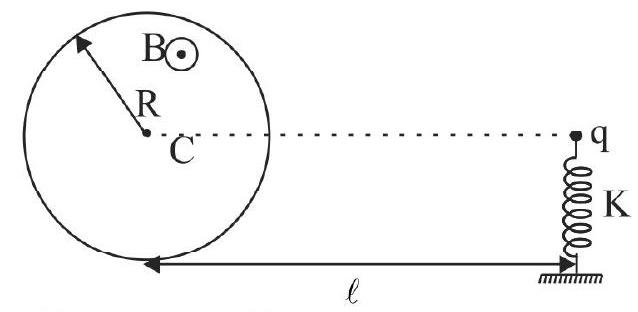
358506
A magnetic field \(B=C_{1} t+C_{2}\) is directed into the plane of paper in the cylindrical volume of radius ' \(r\) '. Here \(C_{1}\) and \(C_{2}\) are positive constants and '\(t\) ' is in seconds. A loop is in the form of an equilateral triangle ' \(ABC\) ' of side length ' \(2r\) ' is placed such that vertex \(C\) lies on the axis of cylindrical region and the plane of loop is perpendicular to the axis. Resistance of unit length of wire is ' \(\lambda\) ' \(\Omega / m\). Find the emf across \(AB\) after some time \(t\).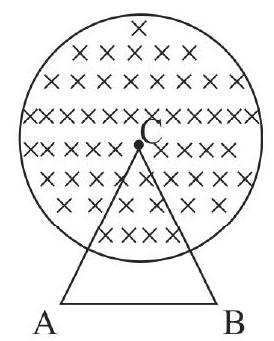
358504
There is a horizontal cylindrical uniform but time varying magnetic field increasing at a constant rate \(dB/dt\) as shown in figure. A charged particle having charge \(q\) and mass \(m\) is kept in equilibrium, at the top of a spring of spring constant \(K\), in such a way that it is on the horizontal line passing through the center of the magnetic field as shown in the figure. The compression in the spring will be
358506
A magnetic field \(B=C_{1} t+C_{2}\) is directed into the plane of paper in the cylindrical volume of radius ' \(r\) '. Here \(C_{1}\) and \(C_{2}\) are positive constants and '\(t\) ' is in seconds. A loop is in the form of an equilateral triangle ' \(ABC\) ' of side length ' \(2r\) ' is placed such that vertex \(C\) lies on the axis of cylindrical region and the plane of loop is perpendicular to the axis. Resistance of unit length of wire is ' \(\lambda\) ' \(\Omega / m\). Find the emf across \(AB\) after some time \(t\).
358504
There is a horizontal cylindrical uniform but time varying magnetic field increasing at a constant rate \(dB/dt\) as shown in figure. A charged particle having charge \(q\) and mass \(m\) is kept in equilibrium, at the top of a spring of spring constant \(K\), in such a way that it is on the horizontal line passing through the center of the magnetic field as shown in the figure. The compression in the spring will be
358506
A magnetic field \(B=C_{1} t+C_{2}\) is directed into the plane of paper in the cylindrical volume of radius ' \(r\) '. Here \(C_{1}\) and \(C_{2}\) are positive constants and '\(t\) ' is in seconds. A loop is in the form of an equilateral triangle ' \(ABC\) ' of side length ' \(2r\) ' is placed such that vertex \(C\) lies on the axis of cylindrical region and the plane of loop is perpendicular to the axis. Resistance of unit length of wire is ' \(\lambda\) ' \(\Omega / m\). Find the emf across \(AB\) after some time \(t\).
358504
There is a horizontal cylindrical uniform but time varying magnetic field increasing at a constant rate \(dB/dt\) as shown in figure. A charged particle having charge \(q\) and mass \(m\) is kept in equilibrium, at the top of a spring of spring constant \(K\), in such a way that it is on the horizontal line passing through the center of the magnetic field as shown in the figure. The compression in the spring will be
358506
A magnetic field \(B=C_{1} t+C_{2}\) is directed into the plane of paper in the cylindrical volume of radius ' \(r\) '. Here \(C_{1}\) and \(C_{2}\) are positive constants and '\(t\) ' is in seconds. A loop is in the form of an equilateral triangle ' \(ABC\) ' of side length ' \(2r\) ' is placed such that vertex \(C\) lies on the axis of cylindrical region and the plane of loop is perpendicular to the axis. Resistance of unit length of wire is ' \(\lambda\) ' \(\Omega / m\). Find the emf across \(AB\) after some time \(t\).
358504
There is a horizontal cylindrical uniform but time varying magnetic field increasing at a constant rate \(dB/dt\) as shown in figure. A charged particle having charge \(q\) and mass \(m\) is kept in equilibrium, at the top of a spring of spring constant \(K\), in such a way that it is on the horizontal line passing through the center of the magnetic field as shown in the figure. The compression in the spring will be
358506
A magnetic field \(B=C_{1} t+C_{2}\) is directed into the plane of paper in the cylindrical volume of radius ' \(r\) '. Here \(C_{1}\) and \(C_{2}\) are positive constants and '\(t\) ' is in seconds. A loop is in the form of an equilateral triangle ' \(ABC\) ' of side length ' \(2r\) ' is placed such that vertex \(C\) lies on the axis of cylindrical region and the plane of loop is perpendicular to the axis. Resistance of unit length of wire is ' \(\lambda\) ' \(\Omega / m\). Find the emf across \(AB\) after some time \(t\).
