358500
There is a uniform magnetic field \(B\) in a circular region of radius \(R\) as shown in figure, whose magnitude changes at the rate of \(dB/dt\). The emf induced across the ends of a circular concentric conducting arc of radius \(R_{1}\) having an angle \(\theta\) as shown \(\left(-O A O^{\prime}=\theta\right)\) is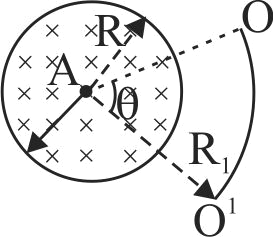
358502
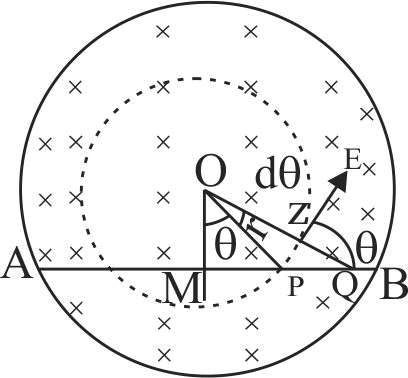
A uniform but time varying magnetic field \(B(t)\) exists in a circular region of radius \(a\) and is directed into the plane of the paper as shown in figure. The magnitude of induced electric field at a point \(P\) at a distance \(r\) from the centre of the circular region
358503
A uniform magnetic field of induction \(B\) fills a cylindrial volume of radius \(R.\) \(A\,{\text{rod}}\,AB\) of length \(2 l\) is placed as shown in figure. If \(B\) is changing at the rate \(dB/dt\) the emf that is produced by the changing magnetic field and that acts between the ends of the rod is
358500
There is a uniform magnetic field \(B\) in a circular region of radius \(R\) as shown in figure, whose magnitude changes at the rate of \(dB/dt\). The emf induced across the ends of a circular concentric conducting arc of radius \(R_{1}\) having an angle \(\theta\) as shown \(\left(-O A O^{\prime}=\theta\right)\) is
358502
A uniform but time varying magnetic field \(B(t)\) exists in a circular region of radius \(a\) and is directed into the plane of the paper as shown in figure. The magnitude of induced electric field at a point \(P\) at a distance \(r\) from the centre of the circular region
358503
A uniform magnetic field of induction \(B\) fills a cylindrial volume of radius \(R.\) \(A\,{\text{rod}}\,AB\) of length \(2 l\) is placed as shown in figure. If \(B\) is changing at the rate \(dB/dt\) the emf that is produced by the changing magnetic field and that acts between the ends of the rod is
358500
There is a uniform magnetic field \(B\) in a circular region of radius \(R\) as shown in figure, whose magnitude changes at the rate of \(dB/dt\). The emf induced across the ends of a circular concentric conducting arc of radius \(R_{1}\) having an angle \(\theta\) as shown \(\left(-O A O^{\prime}=\theta\right)\) is
358502
A uniform but time varying magnetic field \(B(t)\) exists in a circular region of radius \(a\) and is directed into the plane of the paper as shown in figure. The magnitude of induced electric field at a point \(P\) at a distance \(r\) from the centre of the circular region
358503
A uniform magnetic field of induction \(B\) fills a cylindrial volume of radius \(R.\) \(A\,{\text{rod}}\,AB\) of length \(2 l\) is placed as shown in figure. If \(B\) is changing at the rate \(dB/dt\) the emf that is produced by the changing magnetic field and that acts between the ends of the rod is
358500
There is a uniform magnetic field \(B\) in a circular region of radius \(R\) as shown in figure, whose magnitude changes at the rate of \(dB/dt\). The emf induced across the ends of a circular concentric conducting arc of radius \(R_{1}\) having an angle \(\theta\) as shown \(\left(-O A O^{\prime}=\theta\right)\) is
358502
A uniform but time varying magnetic field \(B(t)\) exists in a circular region of radius \(a\) and is directed into the plane of the paper as shown in figure. The magnitude of induced electric field at a point \(P\) at a distance \(r\) from the centre of the circular region
358503
A uniform magnetic field of induction \(B\) fills a cylindrial volume of radius \(R.\) \(A\,{\text{rod}}\,AB\) of length \(2 l\) is placed as shown in figure. If \(B\) is changing at the rate \(dB/dt\) the emf that is produced by the changing magnetic field and that acts between the ends of the rod is