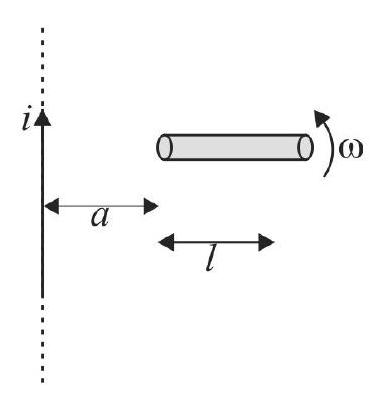
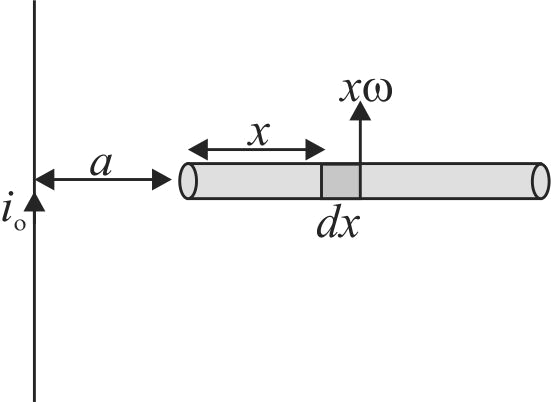
358440 A rod of length \(\ell\) rotates with a uniform angular velocity \(\omega\) about an axis passing through its middle point but normal to its length in a uniform magnetic field of induction \(B\) with its direction parallel to the axis of rotation. The induced \(E M F\) between the two ends of the rod is:
358440 A rod of length \(\ell\) rotates with a uniform angular velocity \(\omega\) about an axis passing through its middle point but normal to its length in a uniform magnetic field of induction \(B\) with its direction parallel to the axis of rotation. The induced \(E M F\) between the two ends of the rod is:
358440 A rod of length \(\ell\) rotates with a uniform angular velocity \(\omega\) about an axis passing through its middle point but normal to its length in a uniform magnetic field of induction \(B\) with its direction parallel to the axis of rotation. The induced \(E M F\) between the two ends of the rod is:
358440 A rod of length \(\ell\) rotates with a uniform angular velocity \(\omega\) about an axis passing through its middle point but normal to its length in a uniform magnetic field of induction \(B\) with its direction parallel to the axis of rotation. The induced \(E M F\) between the two ends of the rod is: