358436 A simple pendulum with bob of mass \(m\) and conducting wire of length \(L\) swings under gravity through an angle \(2 \theta\). The earth's magnetic field component in the direction perpendicular to swing is \(B\). Maximum potential difference induced across the pendulum is: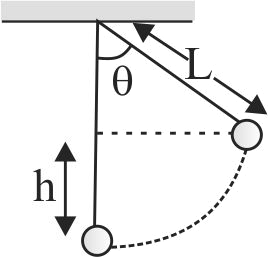

358437 Two identical conducting rings \(A \& B\) of radius \(r\) are in pure rolling over a horizontal conducting plane with same speed (of center of mass) \(u\) but in opposite direction. A constant magnetic field \(B\) is present pointing inside the plane of paper. Then the potential difference between the highest points of the two rings, is

358438 Assertion :
The induced emf in a conducting loop of wire will be non zero when it rotates in a uniform magnetic field.
Reason :
There is change in magnetic flux in this scenario.

358439 A circular coil of mean radius of \(7\;\,cm\) and having 4000 turns is rotated at the rate of 1800 revolutions per minute in the earth's magnetic field ( \(B=0.5 \times 10^{-4}\) gauss), the maximum e.m.f induced in coil will be:

358436 A simple pendulum with bob of mass \(m\) and conducting wire of length \(L\) swings under gravity through an angle \(2 \theta\). The earth's magnetic field component in the direction perpendicular to swing is \(B\). Maximum potential difference induced across the pendulum is:

358437 Two identical conducting rings \(A \& B\) of radius \(r\) are in pure rolling over a horizontal conducting plane with same speed (of center of mass) \(u\) but in opposite direction. A constant magnetic field \(B\) is present pointing inside the plane of paper. Then the potential difference between the highest points of the two rings, is

358438 Assertion :
The induced emf in a conducting loop of wire will be non zero when it rotates in a uniform magnetic field.
Reason :
There is change in magnetic flux in this scenario.

358439 A circular coil of mean radius of \(7\;\,cm\) and having 4000 turns is rotated at the rate of 1800 revolutions per minute in the earth's magnetic field ( \(B=0.5 \times 10^{-4}\) gauss), the maximum e.m.f induced in coil will be:

358436 A simple pendulum with bob of mass \(m\) and conducting wire of length \(L\) swings under gravity through an angle \(2 \theta\). The earth's magnetic field component in the direction perpendicular to swing is \(B\). Maximum potential difference induced across the pendulum is:

358437 Two identical conducting rings \(A \& B\) of radius \(r\) are in pure rolling over a horizontal conducting plane with same speed (of center of mass) \(u\) but in opposite direction. A constant magnetic field \(B\) is present pointing inside the plane of paper. Then the potential difference between the highest points of the two rings, is

358438 Assertion :
The induced emf in a conducting loop of wire will be non zero when it rotates in a uniform magnetic field.
Reason :
There is change in magnetic flux in this scenario.

358439 A circular coil of mean radius of \(7\;\,cm\) and having 4000 turns is rotated at the rate of 1800 revolutions per minute in the earth's magnetic field ( \(B=0.5 \times 10^{-4}\) gauss), the maximum e.m.f induced in coil will be:

358436 A simple pendulum with bob of mass \(m\) and conducting wire of length \(L\) swings under gravity through an angle \(2 \theta\). The earth's magnetic field component in the direction perpendicular to swing is \(B\). Maximum potential difference induced across the pendulum is:

358437 Two identical conducting rings \(A \& B\) of radius \(r\) are in pure rolling over a horizontal conducting plane with same speed (of center of mass) \(u\) but in opposite direction. A constant magnetic field \(B\) is present pointing inside the plane of paper. Then the potential difference between the highest points of the two rings, is

358438 Assertion :
The induced emf in a conducting loop of wire will be non zero when it rotates in a uniform magnetic field.
Reason :
There is change in magnetic flux in this scenario.

358439 A circular coil of mean radius of \(7\;\,cm\) and having 4000 turns is rotated at the rate of 1800 revolutions per minute in the earth's magnetic field ( \(B=0.5 \times 10^{-4}\) gauss), the maximum e.m.f induced in coil will be: