322281
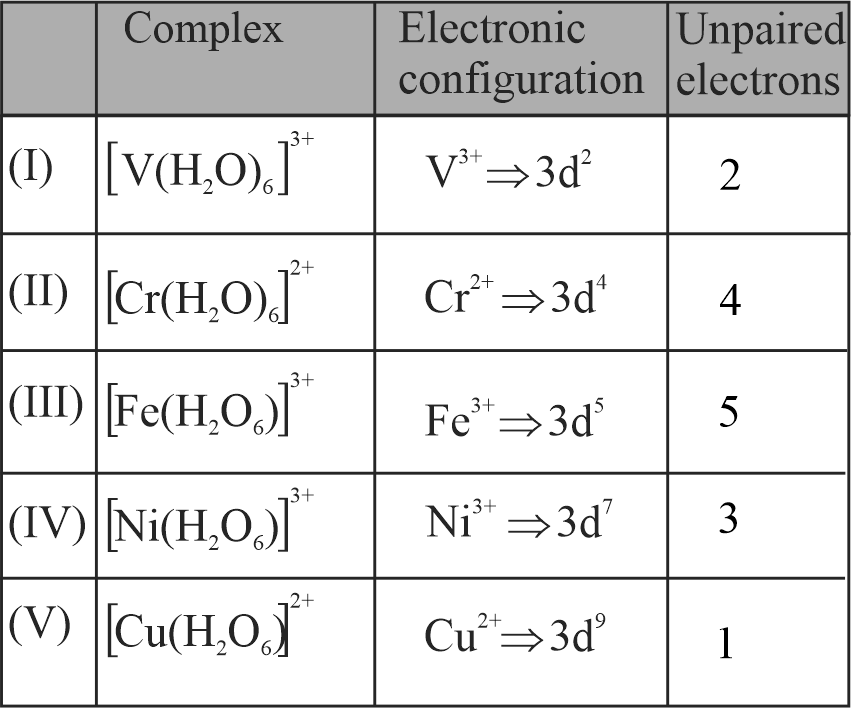
Number of complexes from the following with even number of unpaired " \({\mathrm{d}}\) " electrons is ____.
\({\mathrm{\left[\mathrm{V}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{3+},\left[\mathrm{Cr}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{2+},\left[\mathrm{Fe}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{3+}}}\), \({\mathrm{\left[\mathrm{Ni}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{3+},\left[\mathrm{Cu}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{2+}}}\)
[Given atomic numbers : \({\mathrm{\mathrm{V}=23, \mathrm{Cr}=24}}\),\({\mathrm{\mathrm{Fe}=26, \mathrm{Ni}=28, \mathrm{Cu}=29]}}\)
322282
The correct statements from following are
(I) The strength of anionic ligands can be explained by crystal field theory.
(II) Valence bond theory does not give a quantitative interpretation of kinetic stability of coordination compounds.
(III) The hybridisation involved in formation of \({\mathrm{\left[\mathrm{Ni}(\mathrm{CN})_{4}\right]^{2-}}}\) complex is \({\mathrm{\mathrm{dsp}^{2}}}\).
(IV) The number of possible isomer(s) of \({\mathrm{\operatorname{cis}\left[\mathrm{PtCl}_{2}(\mathrm{en})_{2}\right]^{2+}}}\) is one.
Choose the correct answer from the options given below
322281
Number of complexes from the following with even number of unpaired " \({\mathrm{d}}\) " electrons is ____.
\({\mathrm{\left[\mathrm{V}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{3+},\left[\mathrm{Cr}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{2+},\left[\mathrm{Fe}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{3+}}}\), \({\mathrm{\left[\mathrm{Ni}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{3+},\left[\mathrm{Cu}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{2+}}}\)
[Given atomic numbers : \({\mathrm{\mathrm{V}=23, \mathrm{Cr}=24}}\),\({\mathrm{\mathrm{Fe}=26, \mathrm{Ni}=28, \mathrm{Cu}=29]}}\)
322282
The correct statements from following are
(I) The strength of anionic ligands can be explained by crystal field theory.
(II) Valence bond theory does not give a quantitative interpretation of kinetic stability of coordination compounds.
(III) The hybridisation involved in formation of \({\mathrm{\left[\mathrm{Ni}(\mathrm{CN})_{4}\right]^{2-}}}\) complex is \({\mathrm{\mathrm{dsp}^{2}}}\).
(IV) The number of possible isomer(s) of \({\mathrm{\operatorname{cis}\left[\mathrm{PtCl}_{2}(\mathrm{en})_{2}\right]^{2+}}}\) is one.
Choose the correct answer from the options given below
322281
Number of complexes from the following with even number of unpaired " \({\mathrm{d}}\) " electrons is ____.
\({\mathrm{\left[\mathrm{V}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{3+},\left[\mathrm{Cr}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{2+},\left[\mathrm{Fe}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{3+}}}\), \({\mathrm{\left[\mathrm{Ni}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{3+},\left[\mathrm{Cu}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{2+}}}\)
[Given atomic numbers : \({\mathrm{\mathrm{V}=23, \mathrm{Cr}=24}}\),\({\mathrm{\mathrm{Fe}=26, \mathrm{Ni}=28, \mathrm{Cu}=29]}}\)
322282
The correct statements from following are
(I) The strength of anionic ligands can be explained by crystal field theory.
(II) Valence bond theory does not give a quantitative interpretation of kinetic stability of coordination compounds.
(III) The hybridisation involved in formation of \({\mathrm{\left[\mathrm{Ni}(\mathrm{CN})_{4}\right]^{2-}}}\) complex is \({\mathrm{\mathrm{dsp}^{2}}}\).
(IV) The number of possible isomer(s) of \({\mathrm{\operatorname{cis}\left[\mathrm{PtCl}_{2}(\mathrm{en})_{2}\right]^{2+}}}\) is one.
Choose the correct answer from the options given below
322281
Number of complexes from the following with even number of unpaired " \({\mathrm{d}}\) " electrons is ____.
\({\mathrm{\left[\mathrm{V}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{3+},\left[\mathrm{Cr}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{2+},\left[\mathrm{Fe}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{3+}}}\), \({\mathrm{\left[\mathrm{Ni}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{3+},\left[\mathrm{Cu}\left(\mathrm{H}_{2} \mathrm{O}\right)_{6}\right]^{2+}}}\)
[Given atomic numbers : \({\mathrm{\mathrm{V}=23, \mathrm{Cr}=24}}\),\({\mathrm{\mathrm{Fe}=26, \mathrm{Ni}=28, \mathrm{Cu}=29]}}\)
322282
The correct statements from following are
(I) The strength of anionic ligands can be explained by crystal field theory.
(II) Valence bond theory does not give a quantitative interpretation of kinetic stability of coordination compounds.
(III) The hybridisation involved in formation of \({\mathrm{\left[\mathrm{Ni}(\mathrm{CN})_{4}\right]^{2-}}}\) complex is \({\mathrm{\mathrm{dsp}^{2}}}\).
(IV) The number of possible isomer(s) of \({\mathrm{\operatorname{cis}\left[\mathrm{PtCl}_{2}(\mathrm{en})_{2}\right]^{2+}}}\) is one.
Choose the correct answer from the options given below