Explanation:
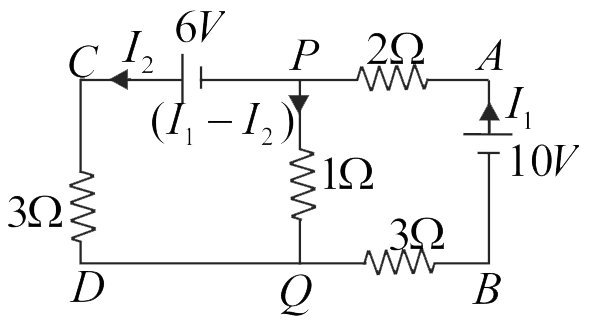
Applying KVL to loop APQBA,
\(2 {I}_{1}+\left({I}_{1}-{I}_{2}\right)+3 {I}_{1}=10\)
\(6 {I}_{1}-{I}_{2}=10\)
\(\therefore \quad {I}_{2}=6 {I}_{1}-10\)\(\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\)
Considering loop \({CDQPC}\),
\(3 {I}_{2}-\left({I}_{1}-{I}_{2}\right)=6\)
\(4 {I}_{2}-{I}_{1}=6\)
Using equation (1),
\(4\left(6 {I}_{1}-10\right)-{I}_{1}=6\)
\(23 \,{I}_{1}-40=6\)
\(\therefore \quad {I}_{1}=\dfrac{46}{23} {~A}\)
\(\therefore \quad {I}_{1}=2 {~A}\)