Explanation:
From the figure, Let potential at point \(O\) is \(x V\), From ohm's law, \(V=I R\)
For loop 1, \(30 - x = 10{\rm{ }}{I_1}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
For loop 2, \(x - 12 = 20{\rm{ }}{I_2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
For loop 3, \(x - 2 = 30{\rm{ }}{I_3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 3 \right)\)
Using \(K C L\) at \(O\)
\(\begin{aligned}& \dfrac{30-x}{10}+\dfrac{12-x}{20}+\dfrac{2-x}{30}=0 \\& \therefore x=20 V\end{aligned}\)
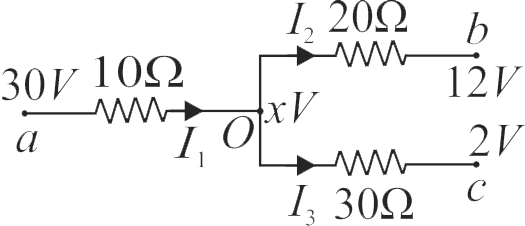
Current through \(20 \Omega\) is \({I_2} = \frac{{20 - 12}}{{20}} = 0.4\;A\)