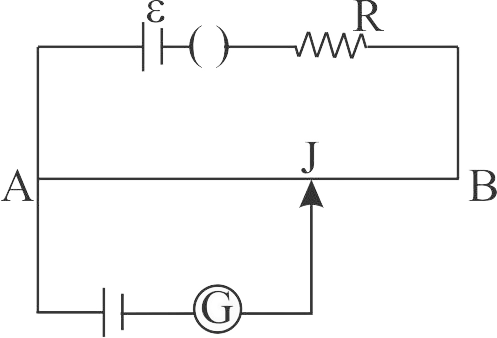
357330 In a potentiometer experiment, when three cells \(A\), \(B\) and \(C\) are connected in series, the balancing length is found to be 740 \(cm\). If \(A\) and \(B\) are connected in series balancing length in 440 \(cm\) and for \(B\) and C connected in series that is 540 \(cm\). Then the emf of \({E_A},{E_B}\;and\;{E_C}\) are respectively (\(K\) is the potential gradient of the rod per unit length, \(K = 1V/Cm\))
357330 In a potentiometer experiment, when three cells \(A\), \(B\) and \(C\) are connected in series, the balancing length is found to be 740 \(cm\). If \(A\) and \(B\) are connected in series balancing length in 440 \(cm\) and for \(B\) and C connected in series that is 540 \(cm\). Then the emf of \({E_A},{E_B}\;and\;{E_C}\) are respectively (\(K\) is the potential gradient of the rod per unit length, \(K = 1V/Cm\))
357330 In a potentiometer experiment, when three cells \(A\), \(B\) and \(C\) are connected in series, the balancing length is found to be 740 \(cm\). If \(A\) and \(B\) are connected in series balancing length in 440 \(cm\) and for \(B\) and C connected in series that is 540 \(cm\). Then the emf of \({E_A},{E_B}\;and\;{E_C}\) are respectively (\(K\) is the potential gradient of the rod per unit length, \(K = 1V/Cm\))
357330 In a potentiometer experiment, when three cells \(A\), \(B\) and \(C\) are connected in series, the balancing length is found to be 740 \(cm\). If \(A\) and \(B\) are connected in series balancing length in 440 \(cm\) and for \(B\) and C connected in series that is 540 \(cm\). Then the emf of \({E_A},{E_B}\;and\;{E_C}\) are respectively (\(K\) is the potential gradient of the rod per unit length, \(K = 1V/Cm\))
357330 In a potentiometer experiment, when three cells \(A\), \(B\) and \(C\) are connected in series, the balancing length is found to be 740 \(cm\). If \(A\) and \(B\) are connected in series balancing length in 440 \(cm\) and for \(B\) and C connected in series that is 540 \(cm\). Then the emf of \({E_A},{E_B}\;and\;{E_C}\) are respectively (\(K\) is the potential gradient of the rod per unit length, \(K = 1V/Cm\))